In the past ten years, there has been a lot of progress in the design of programming models for parallel graph algorithms and their implementation on a variety of hardware platforms including multicore CPUs and GPUs.

Vertex programs for graph analytics

For the most part, this research has focused on vertex programs for graph analytics , which is the study of structural properties of graphs. Page-rank, which is used by Internet search engines to rank web-pages, is a well-known example of a graph analytics computation.

Vertex programs work by assigning application-specific labels to nodes and then iteratively updating the label of each node using the labels of its immediate neighbors in the graph, until a quiescence condition is reached.  To understand how vertex programs work, consider the classical Bellman-Ford algorithm for the single-source shortest-path (sssp) problem. Given an undirected graph in which each edge (u,v) has a positive length l(u,v), the sssp problem is to compute the length of the shortest path from a given source node to every other node in the graph.

In the Bellman-Ford algorithm, the label d(u) of a node u keeps track of the distance of the shortest known path from the source node to that node, and it is initialized to a large positive number except at the source node where it is initialized to zero. The algorithm operates in rounds. In each round, the relaxation operator is applied to every node u: each neighbor v of u is examined, and d(u) is lowered to d(v)+l(v,u) if this value is smaller than d(u). The algorithm terminates if no node changes value in a round. Parallelism can be exploited in each round by applying the operator to multiple nodes simultaneously.

Several variations of this basic theme have been explored. For example, instead of applying the operator to all nodes in a round, some implementations apply the operator only to neighbors of nodes whose labels changed in the previous round. Other implementations keep two labels old and new on each node; in each round, the old labels are read and the new labels are written, avoiding data races.

Vertex programs have been used to solve many graph analytics problems including breadth-first labeling, single-source shortest-path computation, page-rank and connected components. Each problem requires a different operator, but the overall structure of the programs is similar.

One limitation of vertex programs is that information diffuses locally one hop at a time in the graph. This is not a significant limitation for low-diameter graphs like power-law graphs since the average number of hops between nodes is quite small. Given the ubiquity of power-law graphs in social networks and the relative simplicity of vertex programs, it is not surprising that literally hundreds of papers have been published in the past ten years exploring efficient implementations of vertex programs on CPUs, GPUs and FPGAs!

Beyond vertex programs

Since vertex programs for graph analytics have been studied quite thoroughly at this point, what is the next big challenge in parallel graph algorithms? The answer depends on whom you ask of course, but here is what I tell people when I am asked this question: let’s work on “EDA 3.0,” a term I first heard from Leon Stok at IBM.

EDA is an acronym for Electronic Design Automation, and it refers to the software tool chain that chip designers use to design and analyze integrated circuits and circuit boards. EDA 1.0 refers to the state of EDA in the 80’s and 90’s when they had point tools for circuit design on workstations. Later, in EDA 2.0, these tools were integrated into complete design flows and implemented on servers. Today, chip designs have become sufficiently complex that there is a need to parallelize the algorithms used in these tool chains. If this is successful, it will be a significant step towards EDA 3.0.

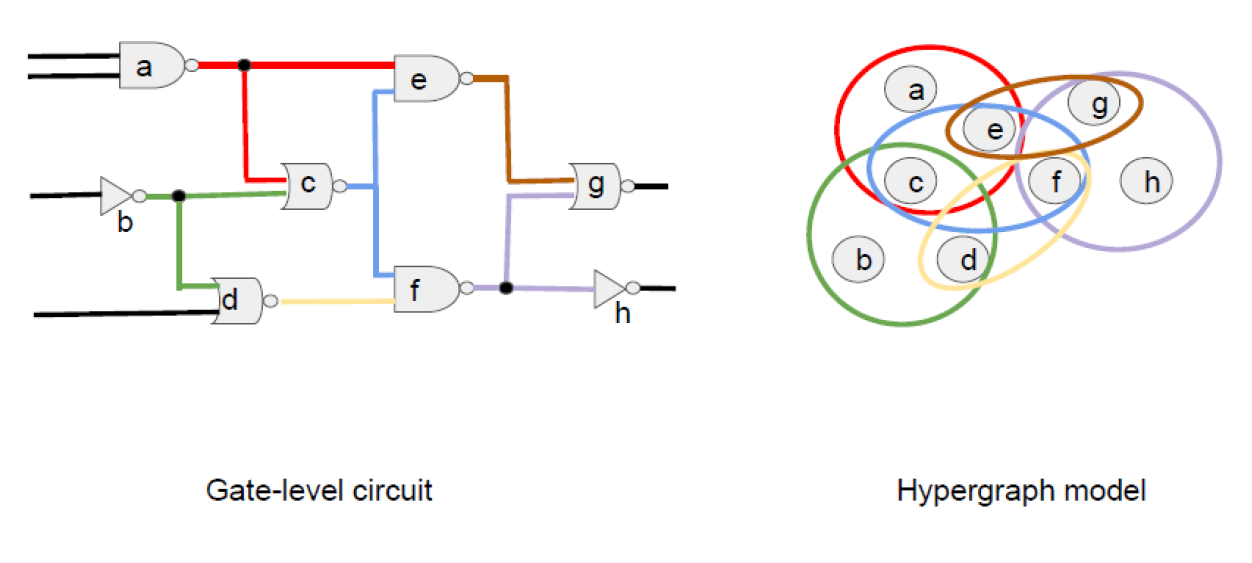
What’s the connection between EDA and graph algorithms?  The key observation is that circuits can be viewed abstractly as graphs or hyper-graphs. The gate-level circuit shown above can be viewed as a graph in which nodes represent gates and edges represent wires between gates. In some problems, it is more useful to view the circuit as a hyper-graph in which all the wires connected the output of a gate are considered to be a single hyper-edge; in the circuit shown above, the output of gate “a” is connected to the inputs of gates “e” and “c”, so there is a hyper-edge connecting nodes {a,c,e} in the abstraction.

With this abstraction, many EDA algorithms for problems like logic synthesis, placement and routing can be viewed as graph or hyper-graph algorithms. For example, logic synthesis is sometimes done by generating And-Inverter Graphs (AIGs) consisting of two-input AND gates and inverters, and then iteratively replacing portions of the circuit with optimized circuits,  using a database of “rewrite rules.” This is similar to peephole optimization in compilers. Parallelism can be exploited by rewriting disjoint portions of the circuit in parallel. Many algorithms for placement are based on hyper-graph partitioning. One popular software package for this is hMetis, which uses a multi-level representation of the hypergraph generated by repeated coarsening. Maze routing algorithms have been parallelized using speculative parallel execution. Timing analysis has been parallelized in the award-winning OpenTimer package using a variation of  DAG scheduling.

None of these algorithms is a vertex program. Moreover circuits are high-diameter graphs so vertex programs are unlikely to work well in any case. There is plenty of room here for innovation and for exploiting what we have learned in the past ten years about implementing parallel graph algorithms.

DARPA IDEA/POSH program

Until recently, research in this area was stymied by the lack of large benchmark circuits for evaluating the quality of placement and routing algorithms for example. The EDA research community also does not have a tradition of releasing artifacts and their conferences do not have an artifact evaluation track, making it difficult to measure progress. On the positive side, there are competitions for problems like timing analysis and placement, associated with their major conferences like ICCAD and DAC.

DARPA’s new IDEA and POSH programs should help in this regard. Among the goals of these programs is to create an open database of large circuit designs for evaluating EDA algorithms, and to implement an integrated and open tool-chain for the entire chip design process.

Let’s become apostles for parallelism and help make EDA 3.0 happen!

About the Author: Keshav Pingali (pingali@cs.utexas.edu) is a professor in the CS department and ICES at the University of Texas at Austin.

 

Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.