The Benefit vs Curse of Specialization
The pervasiveness of deep neural network (DNN) accelerators and cambrian explosion in AI accelerator chip designs is testament to the value of specialization. The datapaths in these accelerators are tailored to the operators and shapes seen in DNN models with support for high parallelism and data reuse, enhancing performance and reducing energy compared to traditional “programmable” alternatives like CPUs and GPUs. Figure 1 is often used to represent this trade-off.
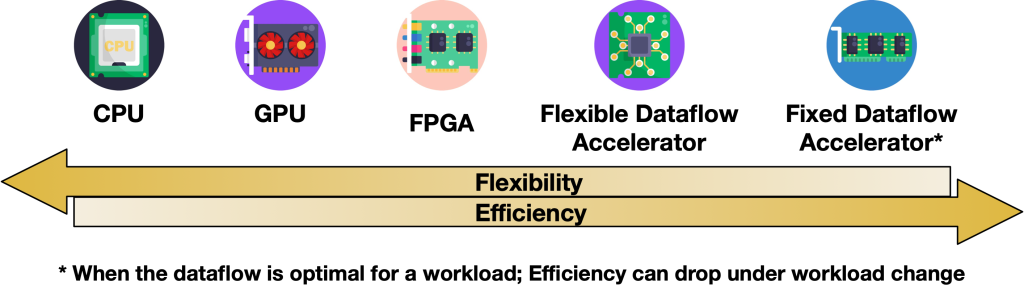
Figure 1. Flexible Accelerator in the Flexibility-Efficiency Space
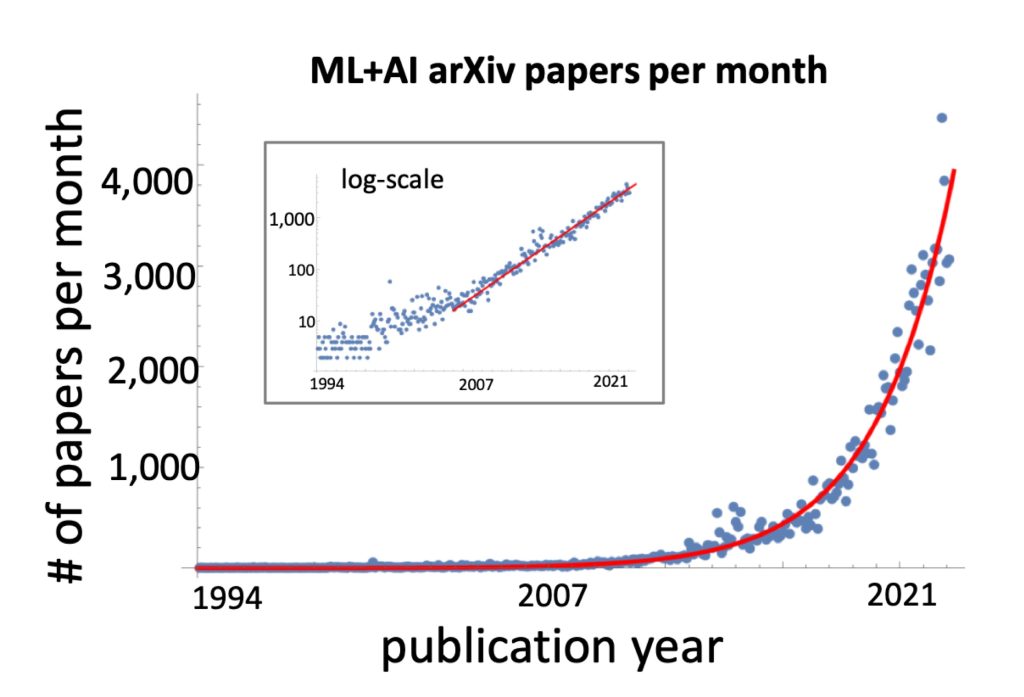
Unfortunately, DNN models are evolving rapidly at an exponential rate, as shown in Figure 2. Even though most DNN operators can be interpreted as Einstein sum operations, the tensor sizes can change dramatically when the DNN model changes. When that happens, it can lead to underutilization of the available hardware resources, reducing performance and energy-efficiency.
Figure 2. Latest trend in the number of new ML + AI papers (Krenn et al., 2023)
To address this challenge, the need for “flexibility” in accelerators is well agreed upon by the architecture community. However, what it means to be flexible is extremely ambiguous today. Flexibility as a term is used loosely today, often interchangeably with programmability and configurability. This means that both a systolic array that can support more than one dataflow and a CGRA like Sambanova are both “flexible” with no clear mechanism of directly comparing them. This hinders systematic exploration of flexible DNN accelerators. In this article, we discuss our attempts to formalize and quantify DNN accelerator flexibility.
Flexibility vs Configurability vs Programmability
We define accelerator flexibility to refer to the HW and SW support for running diverse mappings for a specific operator. A “mapping” refers to the way in which the operator is scheduled over the underlying hardware over space and time. Figure 3 shows an example mapping of a matrix multiplication ( [M=8, K=6] @ [K=6, N=4] ) on a six-processing element (PE) accelerator. Several tools exist today (e.g., Timeloop, CoSA, dMazeRunner, GAMMA, AutoTVM, Interstellar, and Mind Mappings) to search for optimal mappings for a given operator on a given hardware which can be used either at design-time or at compile-time. This flexibility is often provided via configurability (e.g., Eyeriss, Flexflow, MAERI, and Eyeriss v2), but it could also be provided via heterogeneity (i.e., built using a set of fixed function blocks). We differentiate flexibility from programmability, which we define as the ability for hardware to run diverse operators. Thus CPUs and GPUs are programmable but most DNN accelerators are not.
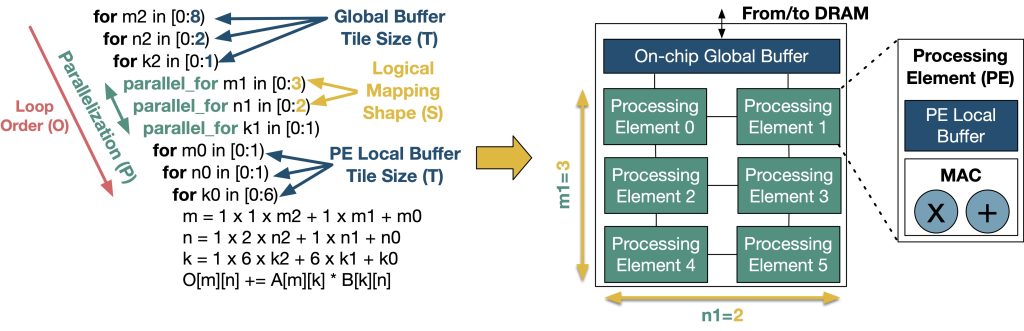
Figure 3. An example mapping of a matrix multiplication on a 3×2-PE accelerator
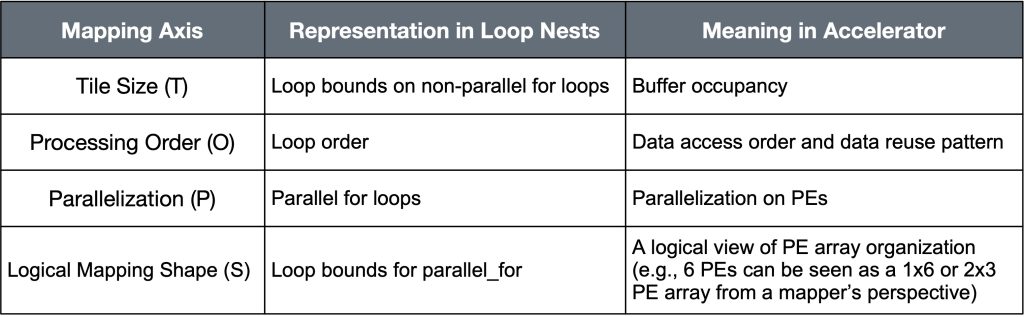
We synthesize learnings from prior work on individual DNN accelerators (e.g., Eyeriss, Flexflow, MAERI, Eyeriss v2, Herald, ShiDianNao, TPUv1,TPUv2 and v3, TPUv4, NVDLA, Dyhard-DNN, Tangram, Simba, Sigma, AI-MT, Planaria, NN-Baton, SARA, MoCA, and INCA) and accelerator design tools (e.g., Timeloop, MAESTRO, MAGNet, DSAGEN, and HASCO) into a formalism for accelerator flexibility. Our formalism measures flexibility along four orthogonal, quantifiable axes – Tile size, Processing Order, Parallelization and Shape – as summarized in Table 1. We use the mnemonic of TOPS to work in conjunction with performance TOPS. A flexible accelerator is one that supports more than one choices within each axis. This formalism subsumes prior accelerator taxonomies like “weight stationary” / “output stationary,” which only captures Processing Order (O) choices.
Table 1. Four mapping axes and their representation in loop nests
HW Support for Flexibility. Flexibility across each axis requires a specific kind of HW support, as shown qualitatively in Figure 4. We discuss the hardware support for the loop order flexibility as an example. Under a memory layout, changing loop order results in non-contiguous memory accesses with an offset. One of the solutions for the problem is as shown in Figure 4 (a), which enables strided accesses. Supporting multiple choices along each axis naturally increases HW cost. Too much flexibility can lead to area and energy overheads from complex reconfigurable logic. On the flip side, insufficient flexibility can also prevent exploiting the beneficial mappings under workload changes, which leads to hardware and energy costs without any return. Therefore, identifying the right amount of flexibility for current and expected workloads is important for designing flexible DNN accelerators.
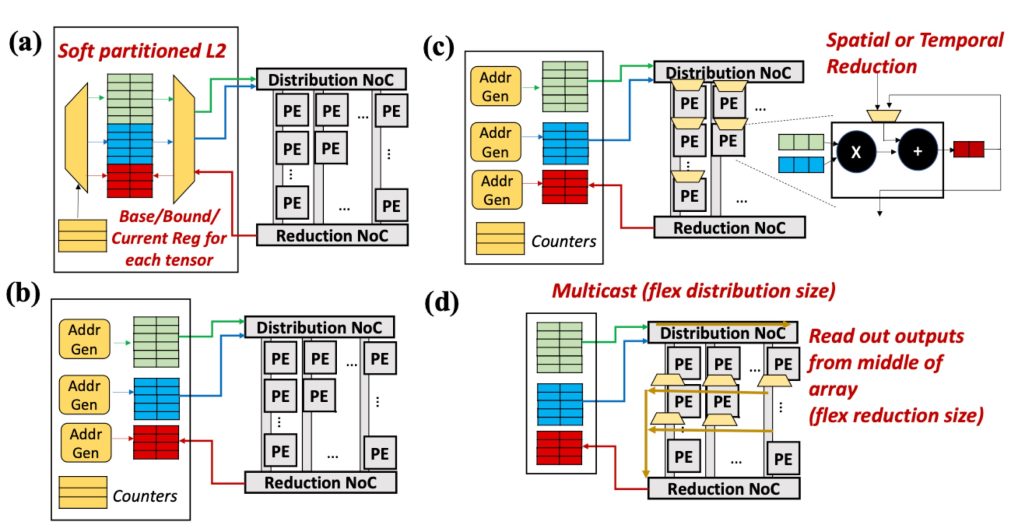
Figure 4. Example hardware components for supporting the four axes of flexibility. (a) tiling (T) flexibility via soft-partitioned scratchpad that can dynamically adjust space for each tensor (b) loop order (O) flexibility via configurable address generator, (c) parallelization (P) flexibility via spatial and temporal reduction support in the PEs, and (d) shape (S) flexibility via flexible network-on-chip (NoC) for dynamic PE grouping.
SW Support for Flexibility. Since each mapping axis corresponds to a parameter in the loop nest, the mapping optimizer in the compiler for a flexible accelerator understands the specific choices for tile sizes, loop order and loop bounds it is allowed to explore when searching for an optimized mapping, as Table 1 shows.
Classification of Flexible Accelerators
Based on the flexibility axis, we can categorize existing accelerator proposals into 16 classes, as shown in Figure 5. For example, TPUv3 supports tiling flexibility only, while NVDLA supports tilling and loop order flexibilities. Based on such capabilities, their classes are encoded into the flexibility dimensions (TOPS): classes 1000 and 1100, respectively. Likewise, we can assign classes for every accelerator, which enables us to have a systematic way to contrast flexible accelerators. Specifically, this also allows designers to explore cost vs benefit trade-offs of individual axes of flexibility.
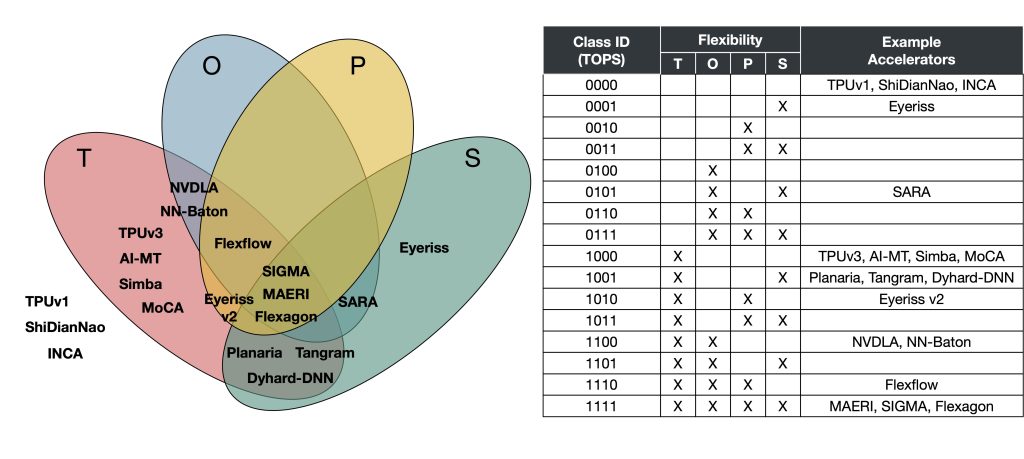
Figure 5. Flexibility plane and corresponding accelerator examples (TPUv1, ShiDianNao, INCA, Eyeriss, SARA, TPUv3, AI-MT, Simba, MoCA, Planaria, Tangram, Dyhard-DNN, Eyeriss v2, NVDLA, NN-Baton, Flexflow, MAERI, Sigma, and Flexagon) . We encode the flexibility information into 4-bit binary flexible accelerator class IDs, as shown in the table on the right.
Quantifying Flexibility
For each flexibility class, we can further quantify the exact amount of flexibility. We propose a metric called Flexion which is defined as the ratio between the number of available mapping choices and the size of the mapping space for each flexibility dimension.
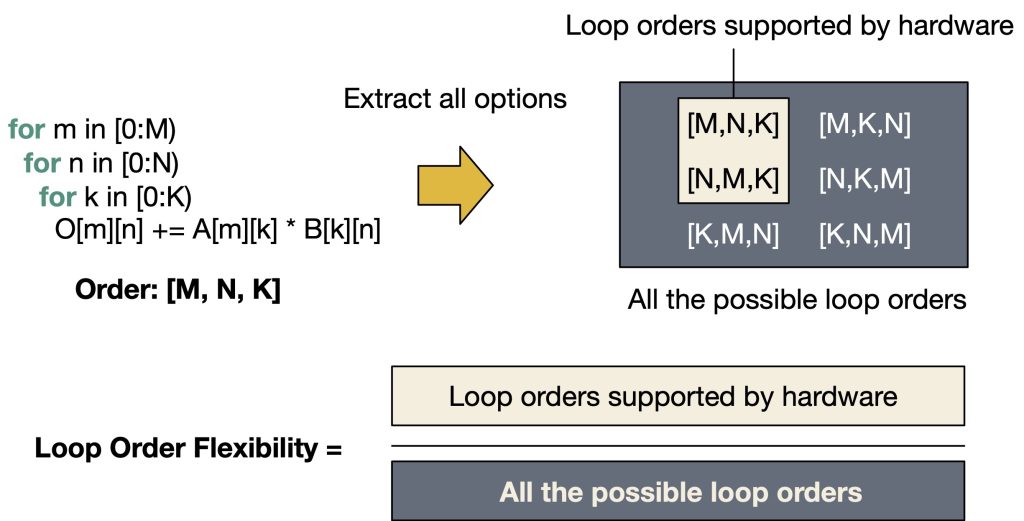
Figure 6. An example loop order flexibility quantization for a matrix multiplication
In Figure 6, we use loop order flexibility as an example to deliver the high-level idea. We assume a single-PE accelerator with a single-level memory hierarchy for simplicity. From the problem, which is a matrix multiplication, we can extract all the possible loop orders, which can be computed as the number of permutations of three dimensions: 3! = 6. Depending on the hardware architecture, an accelerator can have constraints on the available loop order choices. For example, if an accelerator’s address generator only generates contiguous addresses on a fixed data layout, the innermost dimension in the loop order must be aligned with that in the data layout. The example in Figure 6 illustrates such an example (K dimension must be in the innermost loop). To quantify the loop order flexibility, we compute the ratio of the number of available options on hardware and the total number of available options for an operator without any constraints, as the example in Figure 6 shows. The loop order flexibility we define measures the percentage of available loop order choices over all the possible choices from a problem (e.g., matrix multiplication), which can be seen as the capability of an accelerator architecture for supporting various loop orders for the problem.
We can compute the flexion for each mapping axis (T, O, P, and S in Table 1) using the same approach. We can then compute the cross-product of all flexions to define a comprehensive Flexion for the entire accelerator, in a range of [0,1]. For detailed formulation, we invite the readers to our recent papers (Kwon et al., 2020 and Kao et al., 2022).
Remaining Challenges and Future Research Opportunities
This article summarized recent efforts in formalizing the design-space for mapping individual CONV2D and GEMM operators on a DNN accelerator. We define flexibility as the portion of the operator’s map-space captured by the accelerator. We believe there is opportunity for the community to formalize additional aspects of flexibility, some of which are discussed next.
- Our formulation tracks flexibility for running one operator at a time (i.e., layer-wise processing). Inter-layer (i.e., fused operator) mapping, which may include the number of operators that can be fused, the granularity of the fused operators, and so on.
- We only considered mapping of GEMM operators. However, many ML models include non-GEMM-based operators such as softmax, ROIAlign in Mask R-CNN, layer normalization, and so on. We need a methodology to quantify the capability of an accelerator system to run various operators to have a better comparison metric beyond ops/J for GEMM-based operators for capturing true end-to-end ML model execution capabilities.
- Our mapping flexibility formulation requires the memory system to be fixed. However, an accelerator can have a runtime-configurable memory hierarchy (e.g., Planaria), which is yet another dimension of flexibility not captured by our formulation.
- Formalizing flexibility support in HW for algorithmic optimization techniques, such as sparsity (e.g., spectrum from NVIDIA’s 2:4 structured sparse tensor cores to Sigma‘s unstructured sparsity) and running mixed precision models, is an open research question.
- Finally, a key open challenge for a flexible accelerator is having proper compiler support. Today, each custom accelerator often requires its own compiler stack. We believe that a systematic approach like the formalism we defined may assist the development of such a common compiler stack to support a wide family of flexible accelerators.
About the authors:
Hyoukjun Kwon is an assistant professor in the Department of Electrical Engineering and Computer Science (EECS) at UC Irvine. His research interests include cross-stack co-design of ML systems (deep learning model – compiler – accelerator architecture) and the automation of the co-design process. Before joining UCI, he worked as a research scientist at Reality Labs at Meta for two years. He received a Ph.D. in Computer Science from Georgia Tech in 2020, and his thesis on deep neural network mapping, data reuse, and communication flows for flexible deep learning accelerators was recognized by the 2021 ACM SIGARCH/IEEE CS TCCA Outstanding Dissertation Award. Hyoukjun is also a recipient of best paper awards and IEEE MICRO Top Picks award.
Tushar Krishna is an Associate Professor in the School of Electrical and Computer Engineering at Georgia Tech. He also serves as an Associate Director for Georgia Tech’s Center for Research into Novel Computing Hierarchies (CRNCH). He has a Ph.D. in Electrical Engineering and Computer Science from MIT (2014). Before joining Georgia Tech in 2015, Dr. Krishna spent a year as a researcher at the VSSAD group at Intel, Massachusetts. Dr. Krishna’s research spans computer architecture, interconnection networks, networks-on-chip (NoC), and deep learning accelerators – with a focus on optimizing data movement in modern computing systems. His research group has developed and maintains several open-source simulation tools for studying single and multi-node systems for AI inference and training. He was inducted into the HPCA Hall of Fame in 2022. He served as the vice program chair for ISCA 2023.
Michael Pellauer is a Senior Research Scientist at NVIDIA in the Architecture Research Group (2015-present). His research interest is building domain-specific accelerators, with a special emphasis on deep learning and sparse tensor algebra. Prior to NVIDIA, he was a member of the VSSAD group at Intel (2010-2015), where he performed research and advanced development on customized spatial accelerators. Dr. Pellauer holds a Ph.D. from the Massachusetts Institute of Technology in Cambridge, Massachusetts (2010), a Master’s from Chalmers University of Technology in Gothenburg, Sweden (2003), and a Bachelor’s from Brown University in Providence, Rhode Island (1999), with a double-major in Computer Science and English.
Dr. Angshuman Parashar is a Senior Research Scientist at NVIDIA. His research interests are in building, evaluating and programming spatial and data-parallel architectures, with a present focus on automated mapping of machine learning algorithms onto tensor-algebra accelerators. Prior to NVIDIA, he was a member of the VSSAD group at Intel, where he worked with a small team of experts in architecture, languages, workloads and implementation to design a new spatial architecture. Dr. Parashar received his Ph.D. in Computer Science and Engineering from the Pennsylvania State University in 2007, and his B.Tech. in Computer Science and Engineering from the Indian Institute of Technology, Delhi in 2002.
Felix Kao is a software engineer in Waymo. Most of his research lies in Deep Learning Accelerators, Design Space Exploration, and Machine Learning. He is passionate about using his knowledge to develop new and innovative ways to accelerate deep learning workloads.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.