Quantum computers, once seen as a remote theoretical possibility, are now a widely accepted and imminent reality. By exploiting the probabilistic rules of quantum physics, quantum computers can leverage Shor’s algorithm to initiate several breakthroughs, including integer factorization. The difficulty of integer factorization is the cornerstone of widely-accepted cryptographic algorithms like Rivest-Shamir-Adleman (RSA), Diffie-Helman, etc. With recent developments in practical quantum computers, these cryptographic algorithms would fail to provide the necessary security for sensitive data. This blog article emphasizes the urgency of Post-Quantum Cryptography (PQC), and summarizes the most popular PQC algorithms to assist computer architects in preparing hardware for these upcoming, demanding workloads.
Aware of this looming quantum threat, NSA announced in 2015 that it intended to switch eventually to an alternative, quantum-resistant scheme, as yet undetermined. This has led to a race within cryptographers to develop quantum-safe algorithms, giving rise to Post-Quantum Cryptography (PQC). The National Institute of Standards and Technology (NIST) has solicited algorithms to help standardize the development and adoption of efficient and secure PQC. We are therefore at a point where many early contestants have been vetted marginally as being efficient and quantum-safe. Therefore, it is a critical time for architects to explore custom hardware designs that can efficiently execute the demanding kernels of PQC. In turn, such an exploration also facilitates hardware-friendly quantum-safe cryptographic algorithms.
Vulnerable algorithms
The goal of all encryption techniques is to garble the information in such a way that no one except the intended recipient can read the data. Most in-the-field cryptographic applications today are based on the difficulty of integer factorization and discrete logarithm problems. One major application is secure, encrypted online transactions, which are made possible by public-key cryptography. Public-key cryptography revolutionized communications in the 1970s by allowing anyone to send an encrypted message that only the recipient can decrypt, without ever having to exchange secret keys. Such algorithms broadcast a public key that is used to encrypt a message, and a secret key that allows only the possessor to decrypt the ciphertext. For instance, consider the following prime factoring problem. While multiplication of two large prime numbers (say, 78173 x 62017 = 4848054941) is easy, it is impractical for traditional computers to factor the product (public key) into the component primes (secret key).
Efficient public-key encryption RSA and Diffie-Hellman key exchange are the two pillars on which contemporary secure-communication stands. With existing algorithms, it takes years to break them with traditional computers. However, that security, as it turns out, comes with an expiration date.
Quantum Computers and Application of Shor’s Algorithm
Traditional computers store information in bits (0 or 1), and their computational complexity is proportional to the number of bits. However, in the quantum realm, information is stored in qubits that exist in both 0 and 1 states simultaneously. So, a quantum computer can simultaneously calculate a bunch of possible answers for a single input by using a quantum superposition. In other words, the computational complexity of quantum computers grows exponentially with the available qubits.
Encrypting data isn’t a guarantee of data protection; it’s a way of making it harder to access. Therefore, when an AT&T researcher Peter Shor revealed an integer factoring algorithm which was amenable to quantum computers, it immediately undermined the security of all existing communications. This means that an attack on current encryption schemes that takes 2000 years of computing (for RSA-768) on an AMD Opteron processor, would now be broken by a quantum computer in hours. With superior powers of quantum computers, RSA and Diffie-Helman armors stand indefensible, and cryptographers across the globe are rushing towards building quantum-resistant schemes.
Hiding Information in Lattices
Among the many approaches towards a quantum-safe mathematical problem, lattice-based schemes are front-runners. Just as the complexity of RSA was built on the difficulty of prime factorization, the security of lattice-based schemes are based on how easy it is to get lost in a lattice, a set of discrete points in a n-dimensional Euclidean space. Given an arbitrary location within the space, it is extremely difficult to get a lattice point unless you know the secret path. This concept can be used to develop problems, like Shortest Vector Problem, Closest Vector Problem, etc., that have no efficient algorithm, classical or quantum, that can solve these problems in better than exponential time, as of today.
Promises of lattices grew when Oded Regev, in 2005, proved that cryptographic schemes based on a problem called Learning with Errors (LWE) are quantum-safe, as long as the Closest Vector Problem is still resilient towards quantum attacks. A simple formulation of hiding information with errors, as described by an article, is depicted in Figure 1(a). It starts with an odd number as the secret key, hides that key by adding small even noise to multiples of it, and publishes a list of such numbers as the public key. The sender can then encrypt the message with this public key, which only the intended receiver can decrypt.
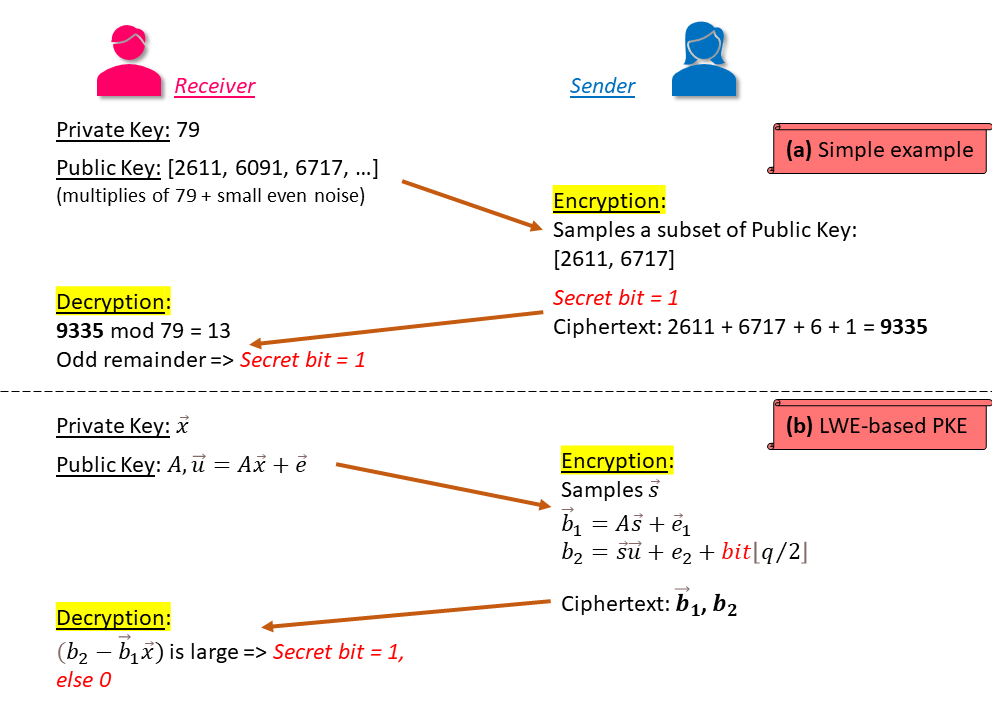
Figure 1: Learning with Errors
In the above formulation, the private key is hidden within a sequence of “approximate” random linear equations on the private key. A more formal definition of LWE-based Public Key Encryption (PKE) is illustrated in Figure 1(b), and stated as follows:
Consider a cryptosystem parameterized by integers n (security parameter), m (number of equations), and q (modulus):
Key Generation: The private key is a n-dimensional vector x⃗ selected randomly, where each value in the vector is an integer between 0 and q. Public key is generated by randomly selecting m samples of another n-dimension vector a⃗i, where i ∈ [1,m], and hiding the private key in it by multiplying a⃗i with x⃗ and adding noise with a small error of ei. Therefore, public key is m samples of (a⃗i, ui = a⃗i⋅ x⃗ + ei), or simply (A, u⃗ = A⋅x⃗ + e⃗).
Encryption/Decryption: Sender encrypts each bit of message using the public keys A and u⃗, and sends the ciphertext to the receiver. Using the private key, the receiver is able to nullify the deviations introduced by encryption, revealing the message.
In depth details of the Public-Key Encryption scheme can be found in this paper.
Computational Complexity
Standard LWE schemes entail various vector/matrix operations, the most complex among which are vector-vector multiplications and vector-matrix multiplications. Hence, it is crucial for an architect to pay more attention to these vector arithmetic while designing hardware to accelerate post-quantum cryptographic schemes. Researchers have proposed, from both the algorithmic and architectural perspective, approaches to accelerate these designs (this 2019 paper summarizes them). However, they still report latencies of at least tens of micro-seconds. Note that classical cryptographic schemes can be typically executed in tens of nano-seconds on contemporary hardware. For instance, FrodoKEM, a standard LWE based NIST candidate, reported latencies around 500 micro-seconds while encrypting on a 3.4GHz Intel i7-6700 processor with AVX2 support.
Additionally, LWE comes with a high ciphertext to plaintext cost, in terms of both storage and computation. Public key is O(mn log q) and encryption increases the size of message by a factor of O(n log q). Researchers soon came up with a more efficient scheme that’s based on “ideal” lattices, and is named Ring-LWE. This is achieved by assuming a structure in the LWE samples (a cyclic structure for Ring-LWE) that reduces the public key size to O(n). Additionally, this assumption also makes the operations amenable to Fast Fourier transform, which can significantly speed up the computations. Studies have reported latencies in the range of 20-30 micro-seconds on FPGAs. Nevertheless, there still exists a large gap between reported latencies and practical deployment requirements, which opens up a golden opportunity for architects to exploit.
About the author: Sarabjeet Singh is a second year PhD student at the University of Utah, interested in hardware security.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


