Sparsity in Deep Neural Networks

The key characteristic of deep learning is that accuracy empirically scales with the size of the model and the amount of training data. Over the past decade, this property has enabled dramatic improvements in the state of the art across a wide range of fields. Naturally, the resources required to train and serve these models scales with model and dataset size. The equivalence of scale to model quality is the catalyst for the pursuit of efficiency in the machine learning and systems community.

A promising avenue for improving the efficiency of deep neural networks (DNNs) is exploiting sparsity. Deep learning workloads are made up of input data, weight matrices that are learned during training, and activation matrices that are computed from the weights and data. Sparsity can arise naturally or be induced in all three of these types of matrices.

Sparsity is exciting because of its generality, but it’s challenging because exploiting it requires innovation at every level of the stack. This post attempts to describe the direction forward for sparsity in deep learning. We start by introducing a model for quantifying the value of exploiting sparsity in an application and then apply it to evaluate research directions in the field.

A Simple Model for the Benefits of Sparsity

Exploiting sparsity can reduce storage, communication and computation requirements. However, the efficiency with which we are able to realize these savings varies for each resource. Additionally, the size of available resources can vary between sparse and dense workloads (e.g., if specialized dense matrix multiplication hardware is available).

Taking these two terms into account, we can model the resource (time, space) requirements of a workload as

Where R represents some resource (storage, communication, computation), W is the amount of work to be done with that resource (in bytes or operations), P is the amount of the resource that is available on the target platform (bytes, bytes/s, ops/s), and E (0 < E ≤ 1) is the efficiency with which we’re able to use that resource.

In practice, we care about the resources we’re able to save relative to dense computation for a given accuracy. Using our model, we can define the realized resource reduction from sparsity as

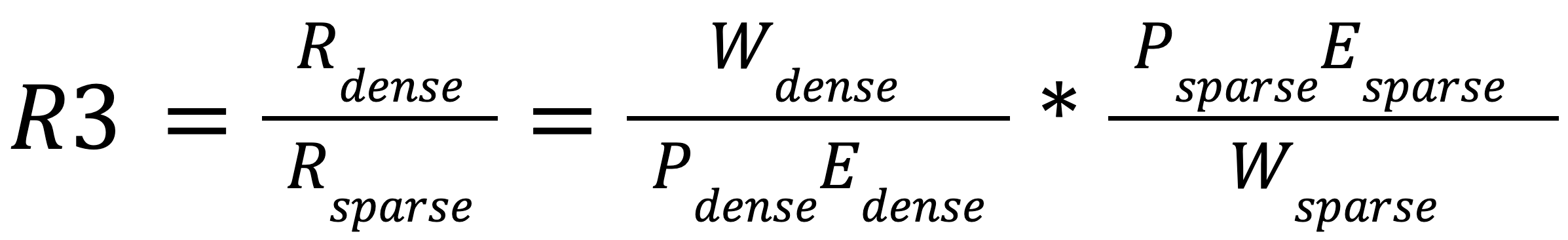
For storage and communication, P_sparse = P_dense and E_dense≅1, since dense tensors can be stored and communicated with no overhead. For compressed sparse tensor formats, it is necessary to save some amount of meta-data to operate on the tensor. Formats like compressed sparse row (CSR) increase storage requirements by ~2x relative to the cost of storing only the nonzero values. Thus, E_{storage, sparse} = ¹⁄₂ for CSR matrices. The efficiency of communicating sparse tensors varies depending on the use case. For example, gradient all-reduce for a weight sparse neural network has E_{comm, sparse} = 1, since only the nonzero values need to be transmitted. For applications where the meta-data needs to be transmitted as well, communication efficiency is equal to the storage efficiency. The storage and communication efficiency of sparse applications come “for free” and are essentially fixed benefits since they only depend on the work reduction provided by sparsity.

For computation, the availability of specialized matrix multiplication hardware places sparsity at a disadvantage. On the latest Nvidia A100 GPU, mixed-precision sparse matrix-dense matrix multiplication (SpMM) peak is ¹⁄₁₆ of the dense matrix multiplication (GEMM) peak. To make matters worse, SpMM kernels achieve less than ¹⁄₃ of peak (E_sparse ≤ ¹⁄₃). GEMM is able to achieve as much as ²⁄₃ of peak. With dense computation possessing significant advantages in hardware capability and efficiency, sparse problems require large reductions in work to realize gains in speed.

The relative importance of compute, communication and storage capacity varies greatly across different workloads. Increased software support will lead to widespread use of sparsity in diverse ways and for different reasons. However, the core challenge with exploiting sparsity in deep learning is computational. If sparsity is to become a dominant technique in these applications, we need to increase its computational advantage (¹/_{Wcompute, sparse}), increase the amount of that advantage we’re able to capture (E_{compute, sparse}), and/or increase hardware capabilities for sparse computation (P_{compute, sparse}).

Harvesting Speed From Sparsity

This section details opportunities for improving the realized resource reduction from sparse neural networks. Table 1 lists the approaches discussed and how they contribute to higher R3_compute in terms of the three contributing factors introduced in the previous section.

Approach	Compute Advantage 1/Wsparse	Compute Efficiency Esparse	Compute Capability Psparse
Sparsification Algorithms	⇧
Sparse Kernels		⇧
Hardware Acceleration			⇧
Structured Sparsity	⇩	⇧	⇧

Table 1: Approaches for improving R3_compute. Upward green arrows denote improvement in a contributing factor. Downward red arrows denote degradation in a factor.

Sparsification Algorithms

One of the most active areas of research in sparse DNNs is algorithms for inducing weight sparsity for training and inference. Improvements in sparsification algorithms enable higher sparsity for the same accuracy, which increases ¹/_Wsparse. The last decade has seen improvements in features like sparse training and sparsity distribution discovery. However, progress on top-end compression ratios has been limited. Table 2 highlights work reductions from different forms of sparsity on popular neural network models.

Model	ResNet-50	EfficientNet-B0	Transformer	Transformer Big
Dataset	ImageNet	ImageNet	ImageNet-64×64	WMT EnDe
Compute Advantage	4.35x	3.32x	2.62x	1.3x
Level of Sparsity	80%	90%	95%	97.5%
Type of Sparsity	weight sparsity	weight sparsity	attention sparsity	ReLU sparsity

Table 2: Sparsity levels and compute advantages on common models. All compute advantages reported for a constant accuracy level on the specified task.

A potential limitation of existing sparse models is that they primarily use building blocks designed for dense models. For dense DNNs, the development of components like batch normalization and multi-head attention were key to improving accuracy. It’s possible that primitives designed specifically to exploit sparsity could enable similar gains.

Beyond weight sparsity, there has recently been increased interest in exploiting activation sparsity. Another promising direction is exploiting activation and weight sparsity simultaneously, which could lead to additional work reductions for a given accuracy.

Sparse Kernels

The workhorse of DNNs is matrix multiplication. In sparse neural networks, matrix multiplication is replaced with SpMM, sampled dense-dense matrix multiplication (SDDMM) or sparse matrix-sparse matrix multiplication (SpGEMM). Improvements in sparse kernels allow us to extract a higher fraction of peak throughput (i.e., increases E_sparse).

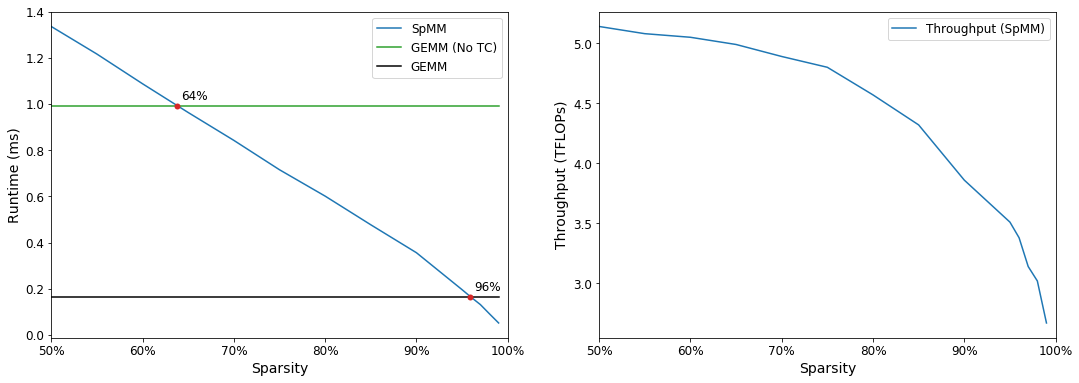Figure 1: (Left) Runtime of sparse matrix-dense matrix multiplication (SpMM) and dense matrix multiplication (GEMM) with increasing sparsity¹. Dense performance reported with and without Tensor Cores. SpMM outperforms GEMM at 64% sparsity without Tensor Core acceleration. With Tensor Cores, SpMM outperforms GEMM at 96% sparsity. (Right) Throughput of SpMM with increasing sparsity. Achieved throughput degrades with increased sparsity due to increased cache misses.

At a high level, state of the art sparse kernels for deep learning parallelize across the rows of the sparse matrix. While this avoids computational irregularity, it limits the reuse of values loaded from the dense operand(s). The only reuse of dense operands across rows of the sparse matrix is through caches. Techniques that parallelize across 2-dimensional regions of the sparse matrix should be able to achieve more reuse and increase throughput across the problem space.

For the sample problem shown in Figure 1, sparse kernels require a compression ratio (^W_dense / _Wsparse) of 25x to outperform hardware accelerated GEMM. For weight-sparse neural networks, 3-5x compression ratios without quality loss are typically achievable (see Table 2). This leaves sparse workloads at a deficit of 5-8.3x. For the problem in Figure 1, sparse kernels achieve 16.7-33% of peak, which bounds the potential gains from kernel improvements at 3-6x. While these numbers are rough, they suggest that improvements in kernels alone will not be sufficient to make weight-sparse neural networks competitive with hardware accelerated dense models.

It’s important to note that this setup is a worst-case scenario for sparsity. More memory-bound problems will see benefits from sparsity at lower compression ratios, and sparsity will likely dominate on platforms without dense matrix multiplication hardware. Beyond weight sparsity, the high sparsity levels found in sparse attention and ReLU activations are sufficient to tilt the scales in favor of sparsity on a wider range of platforms. As algorithms, software and hardware improve, sparsity will bite off a greater and greater fraction of the problem space.

Hardware Acceleration

Hardware specialization has been key to scaling deep learning applications. Sparse hardware accelerators could significantly increase the realized resource reduction from sparsity by increasing sparse compute capabilities (P_sparse).

While much of the conversation often focuses on wholesale specialization to sparse workloads, small-scale investments in balancing existing architectures and adding features for sparse kernels could go a long way towards realizing practical gains from sparsity in the short-term. 

Other near-term opportunities include exploiting new architectures that aim to provide strong support for sparse computation. As these systems mature, they could tip the scale in favor of sparse computation. Nvidia has also added hardware acceleration for a limited form of sparsity that targets inference workloads in their latest Ampere architecture.

Looking to the future, the research community has continued to produce new and interesting architectures for accelerating sparse computation. In the long-term, more research is needed into how we should design processors for sparse computation. Advances in hardware will be a significant contributor to realizing the potential of sparsity in deep learning.

Structured Sparsity

Enforcing structure on the nonzero values in sparse neural networks presents an interesting tradeoff. While the achievable compression ( ¹/_Wsparse) decreases with the constraint on the sparse topology, the additional structure can be exploited to improve compute efficiency (E_sparse) and enable the use of dedicated hardware for matrix multiplication (i.e., increase P_sparse).

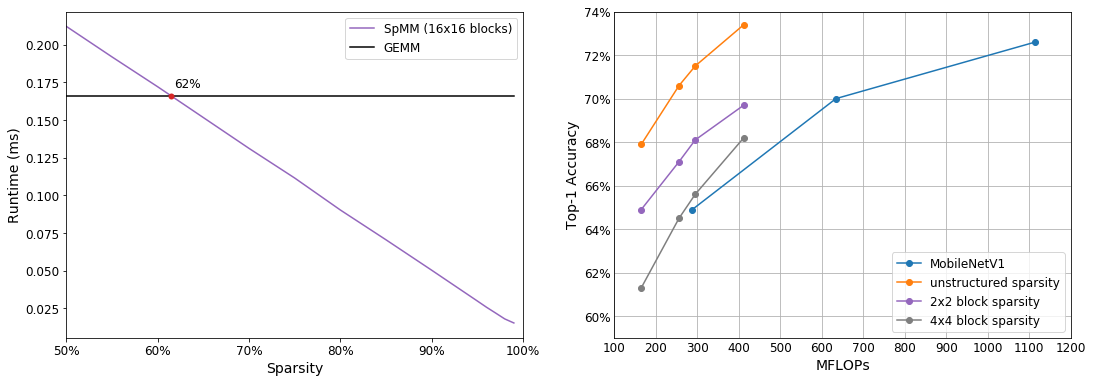Figure 2: (Left) Runtime of block sparse SpMM and GEMM with increasing sparsity². Block sparse SpMM can exploit Tensor Cores to outperform GEMM at 62% sparsity. (Right) FLOP-Accuracy tradeoff curves for sparse MobileNetV1 trained on ImageNet with different sized blocks. Achievable compression for a given accuracy degrades with increasing amounts of structure.

Currently, the most practical form of structured sparsity is block sparsity, which can make use of dense matrix multiplication hardware. The left side of Figure 2 shows the performance of block sparse SpMM on an Nvidia V100 GPU. By exploiting Tensor Cores, sparsity is able to outperform hardware accelerated dense computation at as low as 62% sparsity. 

However, achieving this level of performance relies on relatively large block dimensions. The right side of Figure 2 shows the work reduction provided by sparsity for varying block sizes with MobileNetV1. While unstructured sparsity provides a 3x reduction in FLOPs for a given accuracy, this advantage quickly degrades to 1.6x for 2×2 blocks, and 1.1x for 4×4 blocks. 

MobileNetV1 is a challenging model to compress because of its small size. However, the direction forward for block sparsity is clear: we need to mitigate quality loss from imposing structure and improve the efficiency of kernels with small block sizes.

The tradeoff presented by structured sparsity highlights a broader question in the co-design of hardware, software and algorithms to exploit sparsity: what fraction of the theoretical gains can we realize without handling the complexity of unstructured sparse matrices? If the entire stack is taken into consideration, it’s possible that the most efficient solution relies on these kinds of tradeoffs.

Conclusion

Exploiting sparsity in deep learning is a complex task, but the opportunity for scaling existing applications and enabling new ones is large. In addition to the topics discussed in this post, increased software and hardware support for sparsity will be an important contributor to progress in the field. New workloads and algorithms will likely help tilt the scales, but this will depend on getting researchers the tools they need to explore. The right combination of progress in these areas could be the key ingredients in making sparsity the next big thing in deep learning. 

About the Author: Trevor Gale is a PhD student at Stanford University and a Student Researcher on the Google Brain Team. He’s interested in next-generation machine learning algorithms and their implications for computer systems.

---

Footnotes

1. Benchmarked on square 4096×4096 matrices in mixed precision on an Nvidia V100 GPU with CUDA 11, driver 418.87.01, graphics clock 1530MHz, and memory clock 877MHz. SpMM kernels from Sputnik, GEMM kernels from Nvidia cuBLAS.
2. Benchmarked on square 4096×4096 matrices in mixed precision on an Nvidia V100 GPU with CUDA 11, driver 418.87.01, graphics clock 1530MHz, and memory clock 877MHz. Block sparse SpMM kernels from Triton, GEMM kernels from Nvidia cuBLAS.

Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.