Since my last post, quantum computing hardware continues to develop at an impressive pace, as seen with the recent announcement of Google’s 72-qubit machine (although no test data has been released yet). Pushing the limits of engineering and technology, these machines will most certainly require software adaptation to device variation, operating errors, and environmental noise. This is one aspect of closing the gap between algorithms and hardware. I will return to this later in this series, but I want to first focus on the issue of software and hardware correctness.
In order to get the most out of scarce quantum resources, researchers will need to “cut corners” as much as possible without compromising correctness. This leads to a strong need for a methodology for verifying the correctness of both quantum software and hardware. Coming up with such a methodology is a bit of a grand research challenge, because we do not yet have reliable quantum hardware and it is exponentially-difficult to simulate quantum computations on classical computers (since a quantum computer’s state space is exponential in the number of its qubits).
We can either adopt testing-based or formal-methods approach to these verification problems (or hybrids of both). Assuming that we will use classical computation for verification, both approaches skirt a fundamental tension between classical simulation of quantum computations and quantum supremacy. If we can efficiently simulate quantum computation on a classical computer, then we have proven that this quantum computation does not demonstrate quantum supremacy! Verification approaches involving too much of an algorithms state space also tread in a similar space. If we are optimistic and assume that some quantum algorithms have supremacy over classical algorithms, then we must come up with restricted verification properties that only require partial simulation or formal verification of a sub-exponential state space.
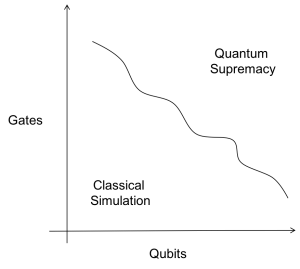
Some results from partial simulation illustrate the subtlety of this boundary between classical simulation and quantum supremacy. Classical computers can simulate quantum algorithms consisting of only “Clifford gates” in time polynomial in the number of qubits used in the algorithm, which proves that these algorithms do not demonstrate quantum supremacy. Algorithms such as Shor’s factoring algorithm, which are exponentially better than known classical algorithms, contain “T gates” (rotations on quantum vectors) as well as Clifford gates. We do not know how to classically simulate Shor’s algorithm in sub-exponential time. We do know, however, how to simulate algorithms consisting of Clifford gates and a very small number of T gates in polynomial time. So the boundary between quantum supremacy and no supremacy is somewhere between a small number of T gates and a lot of T gates in an algorithm. Verification through simulation might exploit the polynomial side of this boundary by trying to define correctness properties that only require simulation of part of an algorithm that contains a small number of T gates. What these properties will be, however, is very much an open area of research.
If we have a simulator or working machine, we can perform end-to-end unit tests or we can invest some extra quantum bits to test assertions. Methods have been developed to test for basic properties such as whether two quantum states are equal, whether two states are entangled, or whether operations commute. Some progress has also been made in applying formal methods to verify quantum computations. QWire uses coq to verify some properties of simple quantum circuits, but classical computation for the theorem prover scales exponentially with the number of qubits. Once again, the key challenge is to define useful correctness properties that a theorem prover can handle more scalably.
We also need tools to understand and characterize the machines that we build. At a basic level, the behavior of quantum devices can be characterized through a process termed quantum tomography , where multiple measurements are used to estimate quantum states. As machines become larger, however, a systems-level approach is needed. Once simple approach would be to compute and uncompute a circuit and use tomography to determine whether a machine returns to its initial state. More sophisticated tests attempt to measure the “quantumness” of a machine and its ability to create entanglement across its qubits.

Once we have functional quantum computers, we may even be able to use quantum algorithms to implement theorem provers and constraint solvers. Yet, we will always be bootstrapping from simulator to hardware, from hardware to larger hardware. This is, of course, similar to our experience with classical microprocessors, but perhaps more challenging since each qubit we add to future machines makes the verification and simulation problem exponentially more difficult for current machines.
About the Author: Fred Chong is the Seymour Goodman Professor of Computer Architecture at the University of Chicago. He is the Lead Principal Investigator of the EPiQC Project (Enabling Practical-scale Quantum Computation), an NSF Expedition in Computing. Many ideas from this blog stem from conversations with the EPiQC team: Margaret Martonosi, Ken Brown, Peter Shor, Eddie Farhi, Aram Harrow, Diana Franklin, David Schuster, John Reppy and Danielle Harlow.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


