Big Data and artificial intelligence have empowered the data-driven computing paradigm, in which data become the most precious resources. Specifically, if one could make use of data not only of herself, but also from other sources to constitute larger datasets, it would likely yield better results. However, sharing data across parties may raise privacy concerns. Indeed, with data becoming increasingly valuable today, companies start to treat data as part of their intelligent properties, and individuals also view their financial and medical data as privacy.
As virtual objects in the digital world, it is difficult to simultaneously allow other parties to make certain authorized use of private data while also ensuring proper protection. If plain (unencrypted) data are exposed to others, there is no easy way to prevent a copy from being stealthily retained for other unauthorized uses. Traditional encryption algorithms can hide secret information, but also prevent further computation on the encrypted data. Essentially, classical data encryption and authentication methods only ensure confidentiality and integrity when the data are statically stored and not additionally processed; they preclude any dynamic transformation of the private data to produce useful results that could be safely released to other parties.
From static data protection to active secure computation
The above dilemma is not impossible to address. Since 1980s, modern cryptography has been developed with various promising approaches to realize such secure and privacy-preserving computing. One of the earliest secure computing proposals is multi-party computation (MPC). It models a scenario where multiple parties each has a piece of secret input data, and they would like to together compute an output result which is exposed to all or some of the involved parties. The protocol must guarantee privacy, meaning that during the process, no party should obtain any information about the original input secret of any other party. A classic example is the Yao’s Millionaires’ Problem, in which two millionaires are interested in knowing who is richer but also not willing to tell each other their actual wealth. MPC can also formalize realistic contemporary scenarios, such as that the service provider offers a proprietary machine learning model and the user queries it with a sensitive input. There are many different realizations of MPC including secret sharing, Yao’s garbled circuits, and protocols based on homomorphic encryption (see below) or oblivious transfers. In particular, recently emerged federated learning could also be viewed as a specialized instance of MPC with weaker security promises.
Another cryptographic primitive that has recently attracted lots of attentions is homomorphic encryption (HE), which is a type of encryption that directly resolves our dilemma by allowing computations on encrypted data. For example, the widely used RSA algorithm is homomorphic with respect to (modular) multiplications. As shown in the figure below, we can multiply the two input RSA ciphertexts to get a new ciphertext, which exactly corresponds to the encryption of the product of the two plaintext values. More sophisticated schemes, such as BGV, FV, and CKKS, are both additive and multiplicative homomorphic, and hence can support general computations by decomposing into these two basic operations. With HE, the data owner could comfortably send the encrypted data to other parties to apply undisclosed algorithms and get the result. As another application case, HE also allows for outsourcing computations to more powerful but untrusted cloud platforms with no data breach risks.
 RSA is homomorphic with respect to (modular) multiplications (modular is omitted in the figure).
RSA is homomorphic with respect to (modular) multiplications (modular is omitted in the figure).
Both MPC and HE realize secure computing in a way that evaluates a function on secret data in a privacy-preserving manner. Zero-knowledge proof (ZKP), on the other hand, can be used to prove certain properties of the secret data, e.g., the secret value x satisfies an equation F(x) = 0. ZKP achieves this by generating a proof that can be verified by other parties, and the proof itself does not leak any information about the secret data, i.e., zero knowledge. These features are particularly desirable when secure computation wants to further demonstrate result integrity, i.e., it is indeed the output of the specified function on the secret that you cannot directly check. For example, a blockchain with anonymous and encrypted transactions can no longer be verified by the public. To solve this, we can additionally require each transaction to also attach a ZK proof to allow for privacy-preserving verification. State-of-the-art and widely adopted ZKP protocols include zk-SNARK used in Zcash, zk-STARK, and more.
Hardware acceleration for modern cryptography
It is well known that cryptography has high demands and sees widespread adoption of specialized hardware acceleration. Modern secure computing algorithms, due to their even higher complexity, exacerbate such demands and become even less friendly to existing general-purpose CPU/GPU platforms.
First, many computations in modern cryptographic primitives are arithmetics over large finite fields, involving not only huge numbers with bit width up to several hundred (e.g., 768-bit), but also complex operations such as modulo a prime and point-add/multiply on elliptic curves. None of these are well supported natively on CPUs or GPUs. Second, although there exists plenty of parallelism in most cryptographic kernels, the dataflow is usually irregular and unbalanced, with complicated and customized optimizations. For example, when computing a dot product on an elliptic curve, each expensive point-multiply is decomposed into various numbers of cheaper point-double and point-add in serial, as shown in the figure below. This results in load imbalance and decreased parallelism. Finally, these algorithms also exhibit large memory footprints and irregular access patterns. Many HE schemes use ciphertext formats that are significantly larger than the original plaintexts, e.g., encrypting an integer into a high-degree polynomial with hundreds of wide-bitwidth coefficients. This makes on-chip caching more expensive and also increases off-chip memory bandwidth pressure. Furthermore, state-of-the-art algorithms to process these polynomials, e.g., number theoretic transforms (NTTs), typically exhibit random and large strided accesses (similar to FFT), making things even more challenging.
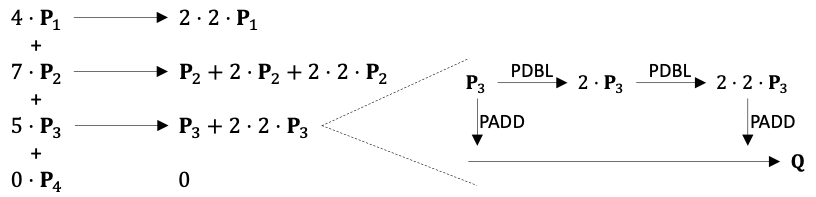 An elliptic curve dot product. A point-multiply is decomposed into a series of point-double and point-add operations based on the scalar’s binary representation.
An elliptic curve dot product. A point-multiply is decomposed into a series of point-double and point-add operations based on the scalar’s binary representation.
Recently, the computer architecture community has seen several attempts to accelerate these secure computing primitives with domain-specific architectures to address the above challenges. An HPCA 2019 paper implements an FPGA-based accelerator for the FV HE scheme, using custom modules for NTTs and other special operations on polynomials. The butterfly access pattern of NTT is fulfilled through an optimized data layout in the on-FPGA block RAMs to avoid conflicts. A later work in ASPLOS 2020, HEAX, accelerates the recently proposed CKKS HE scheme, which is particularly designed for low-precision approximate arithmetics that fit in machine learning applications. The key operation in CKKS is still NTT. HEAX uses a set of on-chip multiplexers sitting in front of the compute units to select the appropriate input elements for each butterfly operation, essentially realizing a carefully crafted on-chip dataflow. And in ISCA 2021, we will present an acceleration architecture for ZKP. It includes much larger-scale NTT modules that extend to off-chip data with a bandwidth-efficient design. It also contains scalable engines for elliptic curve dot products, which effectively avoid the aforementioned load imbalance and resource underutilization issues with dynamic task dispatching and resource sharing.
There are still plenty of challenges and opportunities
These early hardware acceleration efforts have demonstrated pretty encouraging results, with one to two orders of magnitude performance improvements. However, considering the huge gap of several thousand times of slowdown between secure computing (e.g., using HE) and unsecure native processing, it is still far from practical massive deployment.
Challenges remain, but opportunities also exist. If we look back into the history, especially the last domain-specific acceleration trend in machine learning, there may be some lessons to be learned. Beyond traditional acceleration approaches, machine learning systems greatly benefit from hardware-algorithm co-design techniques ranging from model pruning, value quantization, to more advanced hardware-aware neural architecture search (NAS). The same methodology may be also applicable to secure computing, if we could carefully select the most suitable algorithm, or even invent new algorithms that are more hardware-friendly. For example, HEAX chooses to accelerate CKKS, which is an improved and much less intense HE algorithm than the conventional FV scheme, but may introduce small errors in results and should be used in noise-robust applications such as machine learning. Combining the horsepower from both algorithmic development and hardware acceleration, it is not unreasonable to expect cryptography to become another domain achieving an over 10,000 times compute capability boost in the near future.
About the author: Mingyu Gao is an assistant professor at the Institute for Interdisciplinary Information Sciences (IIIS) at Tsinghua University. His research interests lie in the fields of computer architecture and systems, including efficient memory architectures, scalable acceleration for data processing, and hardware security.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.