DNN training is emerging as a popular compute-intensive workload. This blog post provides an overview of the recent research on numerical encoding formats for DNN training, and presents the Hybrid Block Floating-Point (HBFP) format which reduces silicon provisioning for DNN training.
With the emergence of big data and the increased integration of deep learning into modern digital platforms, real-world applications of deep neural networks (DNNs) have become ubiquitous. International Data Corporation (IDC) forecasts AI services to have a five-year Compound Annual Growth Rate (CAGR) of 18.4% with revenues reaching $38 billion in 2024.
While DNNs and data are exploding in size, Moore’s Law is slowing down, steering researchers and vendors away from general-purpose platforms and towards accelerator design. Unfortunately, the two workloads laying the foundation for DNNs have vastly diverse computational and storage requirements, resulting in divergent accelerator designs. Inference workloads use DNN models to predict an outcome. These workloads are online, have tight query latency constraints, but are highly tolerant to error. The net result is that inference workloads lend themselves well to low-precision arithmetic, yielding accelerator designs with high computational density.
In contrast, training workloads run offline to create DNN models (for use in inference), but rely on higher precision arithmetic, leading to accelerator design with both lower computational density and higher requirements for operand storage, bandwidth, and power. As an example, Google targeted inference with TPUv1 using 8- and 16-bit fixed-point arithmetic, used custom floating-point in TPUv2 and v3 for training, and has now included custom cores in TPUv4 for inference and training, that use varying numerical encoding formats.
The salient feature of training algorithms requiring higher arithmetic precision is an algorithmic step known as backward propagation. Backward propagation not only dominates the execution time in training but also demands a wide range from the underlying numerical representation. The latter is due to the trained values in the model being gradient-based with widely varying magnitudes, necessitating the use of floating-point. Unfortunately, floating-point arithmetic requires mantissa realignment and normalization, making floating-point hardware less dense, less power-efficient, and more area-costly than fixed-point hardware.
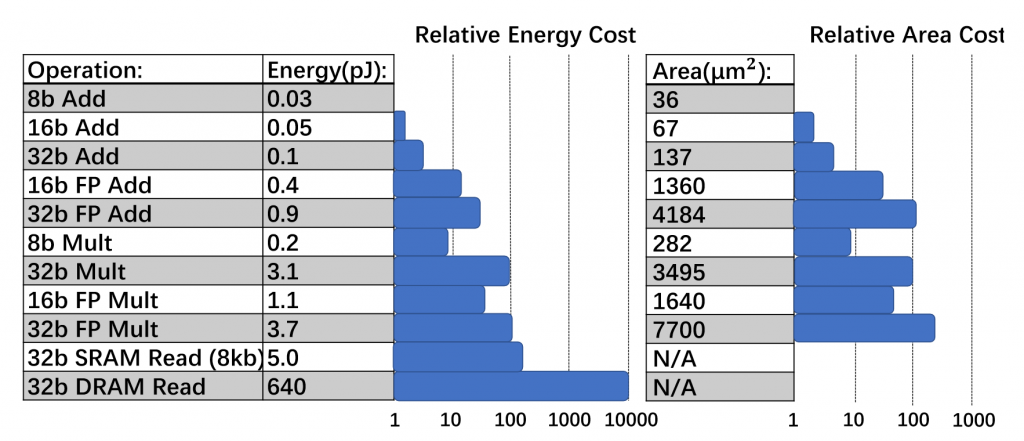
Figure 1: Comparison of energy and relative area costs for different precision for 45nm technology. (source: A Survey of Quantization Methods for Efficient Neural Network Inference)
Figure 1 shows the relative area and energy costs of hardware logic and memory operations for various precisions in a 45nm technology. The figure illustrates that fixed-point and low-precision floating-point logic is significantly more efficient in area and energy than full-precision logic (e.g., 8-bit fixed-point addition is 30x more energy efficient and 116x more area efficient than FP32 addition).
Numerical solutions for training
The conventional numerical encoding for training is FP32 (IEEE 754 format), which is single-precision floating-point with a [sign, exponent, mantissa] format of [1, 8, 23] bits. FP16 (IEEE 754 format), which is half-precision floating-point with a [sign, exponent, mantissa] format of [1, 5, 10] bits, has emerged as a popular denser alternative to FP32. NVIDIA’s mixed-precision training introduces a new trend in deep learning to use FP32 (e.g., for weight updates) together with FP16 to recover data loss.
In recent years, there have been many attempts at training with low-precision number formats. The latest innovation in numerical encoding as a drop-in replacement for FP32 in accelerators is BFLOAT16. This encoding uses the same number of exponent bits as FP32 with half the number of overall bits. Researchers are also training models with FP8, either by limiting its use to specific operands in mixed precision training or customizing its format for the forward vs. back propagation steps by varying the number of bits provisioned for the exponent/mantissa in hybrid FP8 format. Recent work suggests that because the back propagation step mostly requires representing the gradients’ magnitudes, it may also be feasible to train with FP4 with three exponent bits and no mantissa in the back propagation step.
To compensate for data loss with low-precision number formats and to minimize reduction in accuracy, many also propose recovery techniques. These include stochastic rounding techniques, loss scaling, maintaining select layers of the network in higher precision, and chunk-based accumulation. These recovery techniques aim to provide enough range and precision to capture the variations in tensor distributions over the course of training. Unfortunately, these techniques have fallen short of broad applicability to address information loss, because they require significant fine-tuning, are not generalizable to all models, and remain an open research problem.
Instead of using low-precision floating-point, recent research advocates the use of Block Floating-Point (BFP), which was first proposed for signal processing algorithms in the 1990’s to improve mobile platform density. BFP is a special case of floating-point which strikes a balance between fixed-point and floating-point representations. The key difference between the BFP format and the floating-point format is that the BFP format shares a single exponent across a block of values, while the floating-point format does not. Figure 2 illustrates the FP and BFP representations of a tensor when the block size is equal to the tensor size. As such, within a block, BFP enforces a fixed-point-like range, whereas different blocks can have different exponents, leading to a wide range of representation. This property enables dot products to be computed with high precision. Moreover, BFP ALUs achieve higher silicon density and energy efficiency than FP ones, because they amortize the exponent management overhead over many values. BFP’s shared exponents enable dense fixed-point logic for multiply-and-accumulate (MAC)-based operations.
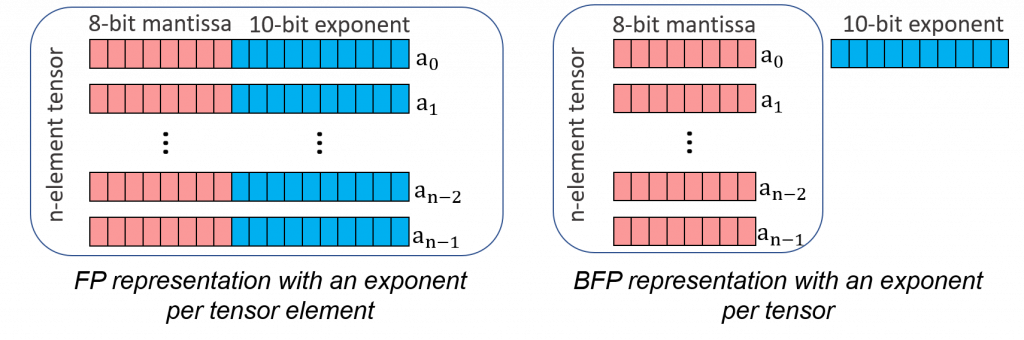
Figure 2: An n-element tensor represented in 8-bit FP and 8-bit BFP (with block size of n).
Recent research advocates the use of BFP for DNN training (and inference in Microsoft’s Brainwave). Flexpoint and Dynamic Fixed-Point (DFP) propose BFP formats for training with a 16-bit mantissa and a shared exponent. Sharing the exponent among a large group of mantissas enables the use of fixed-point arithmetic for the majority of DNN operations and dramatically reduces operand storage, movement energy and bandwidth requirements. Unfortunately, the use of BFP remains an open research problem because not all DNN training operations lend themselves well to grouping mantissas, resulting in overall inferior accuracy as compared to floating-point.
Training DNNs with Hybrid Block Floating-Point
In a NeurIPS 2018 paper, the authors propose a mixed-precision format for training using BFP, called Hybrid Block Floating-Point (HBFP). HBFP uses 8-bit BFP for tensors in the training operations which lend themselves well to grouping (e.g., dot products, convolutions), and FP32 for the remaining operations (e.g., activations, regularizations). HBFP is superior to training with pure BFP for two reasons. First, using BFP for all operations may result in divergence unless wide mantissas are employed. Second, general-purpose BFP operations have high area overhead. HBFP builds on the insight that specific DNN operations (e.g., activations, regularizations) cannot tolerate BFP inputs, because those operations often result in wide tensor distributions that can be too wide for BFP, leading to loss of values at the edge of the distributions. Thus, not all operations can tolerate taking BFP values as inputs, as they may change the value distributions in non-trivial ways, with both small and large values impacting the results. However, dot products —which dominate DNN training— are resilient to such data loss. Dot products are reductions, and thus the largest values in the input tensors dominate the sum, with small values having little impact on the final result. Therefore, HBFP judiciously uses FP32 only for operations that require it, and provides an area-efficient numerical representation for the others.
HBFP is an arithmetic representation for DNN training that preserves accuracy and convergence rate, with ALU density and energy efficiency similar to representations used in inference accelerators. HBFP training results have been shown to match the accuracy attainable by FP32 (see Table 1 and Table 2) while achieving 8.5x higher throughput and 4x more compact models.
| Dataset | Model | FP32 | HBFP8 |
| CIFAR100 | ResNet-50 | 26.07% | 25.12% |
| WideResNet-28-10 | 20.35% | 20.78% | |
| DenseNet-40 | 26.03% | 26.27% | |
| SVHN | ResNet-50 | 1.89% | 1.98% |
| WideResNet-16-8 | 2.00% | 1.98% | |
| DenseNet-40 | 1.80% | 1.79% | |
| ImageNet | ResNet-50 | 23.64% | 23.88% |
Table 1: Test error of image classification models. HBFP8 indicates a setting with 8-bit mantissas and 16-bit weight storage.
| Dataset | Model | FP32 | HBFP8 |
| Penn Tree Bank(PTB) | LSTM | 61.3 | 61.9 |
| English Wikipedia | BERT-Tiny | 60.9 | 62.9 |
| BERT-Medium | 10.68 | 11.50 | |
| BERT-Base | 7.77 | 8.14 |
Table 2: Validation perplexity of language modeling models. HBFP8 indicates a setting with 8-bit mantissas and 16-bit weight storage.
The ColTraIn (Co-located DNN Training and Inference) project at EPFL has recently released the HBFP Training Emulator. We foresee HBFP laying the foundation for accurate training algorithms running on accelerators with an order of magnitude denser arithmetic than conventional or novel floating-point-based platforms. The ColTraIn emulator repository includes several example DNN models including CNNs (ResNet, WideResNet, DenseNet, AlexNet), LSTMs, and BERT for both HBFP and a reference FP32 baseline.
About the authors:
Simla Burcu Harma is a second-year PhD student at Computer and Communication Sciences, EPFL, and a doctoral research assistant at PARSA under the supervision of Prof. Babak Falsafi. Her research is focused on novel numerical encodings for deep learning and Machine Learning accelerators.
Mario Drumond is a Chief Technology Officer in a stealth startup. He completed his PhD thesis at Computer and Communication Sciences, EPFL, advised by Prof. Babak Falsafi. His research interests include Machine Learning accelerators, near memory processing, and FPGA acceleration.
Babak Falsafi is a Professor in the School of Computer and Communication Sciences and the founding director of EcoCloud, an industrial/academic consortium at EPFL investigating technologies to increase efficiency and reduce emissions in datacenters. His research interests include computer architecture, datacenter systems, design for dark silicon, robust methodologies for computer system design and evaluation.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


