Quantum computing sits poised at the verge of a revolution. Quantum machines may soon be capable of performing calculations in chemistry, physics, and other fields that are extremely difficult or even impossible for today’s computers. Yet there is a significant gap between the theory of quantum algorithms and the devices that will support them. Architects and systems researchers are needed to fill this gap, designing machines and software tools that will efficiently map quantum applications to the constraints of real physical machines.
Recent progress in quantum hardware has been impressive. IBM is testing a machine with 50 quantum bits (qubits). Google and Intel have plans to build similar scale machines in the near future. Machines up to 100 qubits are around the corner, and even 1,000 qubits appears buildable. John Preskill, a long-time leader in quantum computing at Caltech, notes that we are at a “priviledged time in the history of science and technology,” Specifically, classical supercomputers can not simulate quantum machines larger than 50-100 quantum bits. Emerging physical machines will bring us into unexplored territory and will allow us to learn how real computations scale in practice.
The key to quantum computation is that every additional qubit doubles the potential computing power of a quantum machine. That doubling, however, is not perfect as these machines will have high error rates for some time come. Preskill has a good term to these exciting, but noisy machines: NISQ (Noisy Intermediate-Scale Quantum computers). Ideally, we would use quantum error correction codes to support error-free quantum computations. These codes, however, require many physical qubits to create a single, fault-tolerant qubit; transforming a 100 qubit machine into 3-5 usable logical qubits. Until qubit resources are much larger, a practical approach would be to explore error-tolerant algorithms and use lightweight error-mitigation techniques. So NISQ machines imply living with errors and exploring the effects of noise on the performance and correctness of quantum algorithms.
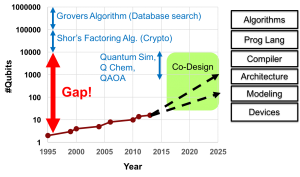
Figure 1: The gap between algorithms and realistic machines.
Additionally, despite technology advances, there remains a wide gap between the machines we expect and the algorithms necessary to make full use of their power. In the Figure 1, we can see the size of physical machines (in this case trapped ion machines) over time. Ground-breaking theoretical work produced Shor’s algorithm for the factorization of the product of two primes and Grover’s algorithm for quantum search, but both would require machines many orders of magnitude larger than currently practical. This gap has led to a recent focus on smaller-scale, heuristic quantum algorithms in areas such as quantum simulation, quantum chemistry, and quantum approximate optimization (QAOA). Even these smaller-scale algorithms, however, suffer from a gap of two to three orders of magnitude from recent machines. Relying on solely technology improvements may require 10-20 years to close even this smaller gap.
A promising way to close this gap sooner is to create a bridge from algorithms to physical machines with a software-architecture stack that can increase qubit and gate efficiency through automated optimizations and co-design. For example, recent work on quantum circuit compilation tools has shown that automated optimization produces significantly more efficient results than hand-optimized circuits, even when only a handful of qubits are involved. The advantages of automated tools will be even greater as the scale and complexity of quantum programs grows. Other important targets for optimization are mapping and scheduling computations to physical qubit topologies and constraints, specializing reliability and error mitigation for each quantum application, and exploiting machine-specific functionality such as multi-qubit or analog operators.
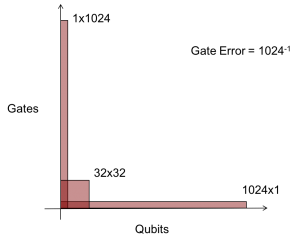
Figure 2: Space-time (quantum volume) constraints on machines due to gate errors.
Although the progress of quantum machines is often measured in terms of qubits, an equally important metric is that of the number of gates (operations) that a machine supports. In fact, the product of qubits times gates would be a more accurate measure of the capabilities of a machine, as shown in Figure 2. For example, if we have gate error of 1 in 1024, that means that we can have a 1-qubit machine that can perform 1024 gates on that qubit before expecting an error. Similarly, we could have 1024 qubits and only perform a single gate. Finally, we could have a more balanced system with 32 qubits, each of which could undergo 32 gate operations. Other details include that 2-qubit gates are more difficult than 1-qubit gates, and that the interconnect between each physical qubit limits the effectiveness of a machine. IBM refers to the effective scaling a quantum machine as its quantum volume. Optimistically, we might hope to see a machine with a quantum volume of 100 qubits times 1,000 gates in the next couple years. So more precisely, the gap between algorithms and machines can be measured in terms of this space-time product and increasing the efficiency of algorithms on machines involves reducing both the number of qubits and gates needed.
The next few blog posts in this series will describe some of the grand research challenges in closing the algorithms-machine gap and achieving practical quantum computing. For those interested in pursuing some of these challenges, I will also provide links to some of the research infrastructure and educational resources available. Much of this material will be presented in tutorial form in June at the International Symposium on Computer Architecture in Los Angeles (learn about quantum algorithms from Peter Shor himself and run code on actual IBM quantum machines!). Tutorial materials will also subsequently be available online.
About the Author: Fred Chong is the Seymour Goodman Professor of Computer Architecture at the University of Chicago. He is the Lead Principal Investigator of the EPiQC Project (Enabling Practical-scale Quantum Computation), an NSF Expedition in Computing. Many ideas from this blog stem from conversations with the EPiQC team: Margaret Martonosi, Ken Brown, Peter Shor, Eddie Farhi, Aram Harrow, Diana Franklin, David Schuster, John Reppy and Danielle Harlow.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


