In a recent IEEE Spectrum article, Mikhail Dyakonov makes The Case Against Quantum Computing, focusing on the idea that building a quantum computer would require precise control over 2300 continuous variables. This view is absolutely correct if we were building an analog quantum computer with an exponential number of parameters, but a modular digital design allows us to use a divide-and-conquer approach that prevents control problems from composing exponentially. This is analogous to how we build scalable classical computers, using digital signals and signal restoration to prevent noise from accumulating across designs involving billions of transistors.
It is tempting to view quantum computing as an analog enterprise, with its exponentially-complex superpositions and probabilistic outcomes of measurement. Remarkably, most quantum computer designs follow a digital discipline (other than the D-Wave quantum annealer, which itself uses a fixed set of control values during its analog annealing process). In particular, this is accomplished through quantum error correction codes and the measurement of error syndromes through ancilla qubits (scratch qubits). Imagine a 3-qubit quantum majority code in which a logical “0” is encoded as “000” and a logical “1” is encoded as “111.” Just as with a classical majority code, a single bit-flip error can be corrected by restoring to the majority value. Unlike a classical code, however, we can not directly measure the qubits else their quantum state will be destroyed. Instead, we measure syndromes from each possible pair of qubits by interacting them with an ancilla, then measure each ancilla. Although the errors to the qubits are actually continuous, the effect of measuring the ancilla is to discretize the errors, as well as inform us whether an error occurred so that it can be corrected. With this methodology, quantum states are restored in a modular way for even a large quantum computer. Furthermore, operations on error-corrected qubits can be viewed as digital rather than analog, and only a small number of universal operations (H, T, CNOT) are needed for universal quantum computation. Through careful design and engineering, error correction codes and this small set of precise operations will lead to machines that could support practical quantum computation.
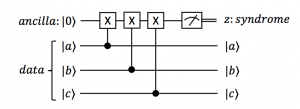
Fig 1: Measuring an error syndrome for data qubits a, b, and c. Time flows from left to right in this quantum circuit diagram. Single lines represent quantum bits and double lines represent classical bits. Each controlled-X operator is a controlled-not in which the value of the data qubit determines whether a quantum not gate operates on the ancilla. The meter represents measurement where classical bit z is the obtained syndrome outcome. If any one of data qubits suffers a bit-flip error, it will change the syndrome outcome and hence be detected.
It is true that quantum error correction codes have historically required enormous overhead that would be impractical for the foreseeable future.
However, this overhead is constantly being reduced through improvements in error-corrected gate methods and reduction in the physical error rates. It is expected that qubit optimized instances of the surface code will demonstrate quantum error correction with 20 qubits in the near term. Surface codes are topological codes that are under-constrained (they also only require near-neighbor 2D qubit connectivity). They are under-constrained in that error syndromes do not uniquely determine the pattern of physical errors that actually occurred. Instead, a maximum likelihood calculation must be computed offline to determine which errors to correct. Intuitively, this under-constrained coding allows more errors to be corrected by fewer physical qubits.
It is also true that high physical error rates in quantum devices can lead to high error-correction overhead, even for surface codes. Physical error-mitigation techniques, however, promise to make devices more reliable and make low-overhead error-correction codes possible. These error-mitigation techniques rely on examining the physical basis of the error. For most solid-state systems, the qubit is designed from more primitive physical elements. An active area of research is combining noisy qubits to generate less noisy qubits at the physical level. On example is a proposed 4-element superconducting ensemble, in which noise continuously transfers from two transmons to two resonant cavities. The noise is then removed from the cavities through a combination of control pulses and dissipation. It is expected that this technique can improve the effective logical qubit lifetimes against photon losses and dephasing error by a factor of more than 40. Another method for physical error mitigation is to use some qubits not for computation but to control the noise source. Trapped-ion machines rely on the shared ion motion to two-qubit gates. A “cooling ion” of a different species can be used to remove noise in the motion to improve the gates between data ions.

Fig 2: A trapped-ion chip for quantum computation (Credit Kai Hudek at IonQ and Emily Edwards at UMD).
In addition to enabling more scalable error-corrected quantum computing, error-mitigation techniques will likely be effective enough to allow small machines of 100-1000 qubits to run some applications without error correction. Additionally, some application-level error-correction is possible. For example, an encoding of quantum chemistry problems, call Generalized Superfast, can correct for a single qubit error. This encoding is one of the most efficient discretizations of fermionic quantum simulation, and thus its error-correction properties come at essentially no extra overhead.
Overall, the outlook for quantum computation is promising due to the combination of digital modular design, error-correction, error-mitigation, and application-level fault-tolerance. Hardware continues to scale in performance, where the most recent example is the ion-trap based quantum computer by IonQ demonstrating limited gate operation on up to 79 qubits with fully connected, high fidelity entangling operation on 11 qubits at a time. Additionally, algorithmic and compiler optimizations show signs of orders-of-magnitude reductions in resources required by quantum applications in terms of qubits, operations, and reliability. A more recent IEEE article reflects this positive outlook.
About the Authors:
Fred Chong is the Seymour Goodman Professor of Computer Architecture at the University of Chicago. He is the Lead Principal Investigator of the EPiQC Project (Enabling Practical-scale Quantum Computation), an NSF Expedition in Computing and a member of the STAQ Project.
Ken Brown is an Associate Professor in ECE at Duke. He is the Lead Principal Investigator of the STAQ Project (Software-Tailored Architecture for Quantum co-design) and a member of the EPiQC Project.
Yongshan Ding is a 3rd-year graduate student on the EPiQC Project advised by Fred Chong. He is co-author (with Fred Chong) of the upcoming Synthesis Lecture in Computer Architecture: Computer Systems Research for Noisy-Intermediate Scale Quantum Computers.
Many ideas from this blog stem from conversations with the rest of the EPiQC team: Ike Chuang, Diana Franklin, Danielle Harlow, Aram Harrow, Margaret Martonosi, John Reppy, David Schuster, and Peter Shor.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


