The term “von Neumann bottleneck” was coined by John Backus in his 1978 Turing Award lecture to refer to the bus connecting the CPU to the store in von Neumann architectures. In this lecture, he argued that the bus was a bottleneck because programs execute on the CPU and must “pump single words back and forth through the von Neumann bottleneck” to perform computations.
Backus’s goal was not to criticize von Neumann architectures but to highlight what he believed was the debilitating influence of this computing model on high-level programming languages (his lecture was titled “Can Programming be Liberated from the von Neumann Style? A Functional Style and its Algebra of Programs”). Pointing out that assignment statements and control-flow constructs in imperative programming languages reflect the existence of the store and the program counter respectively in von Neumann architectures, he proposed to eliminate these constructs entirely from programming languages, particularly for parallel computing.
In his words, “The assignment statement is the von Neumann bottleneck of programming languages and keeps us thinking in word-at-a-time terms in much the same way the computer’s bottleneck does.”
Instead of imperative languages, Backus advocated using functional languages, and he described a functional language called FP and an algebra for FP based on rewrite rules. An FP program is executed by rewriting it repeatedly using these simplification rules until it cannot be rewritten further. Parallelism can be exploited by rewriting different parts of the program simultaneously, and his lecture mentioned efforts by his collaborators to build a massively parallel tree machine that directly executed FP programs, using repeated rounds of parallel parsing and rewriting.
Backus’s lecture is probably the most highly cited Turing award lecture, and his imprimatur gave a boost to research in functional languages and “non von-Neumann architectures” like dataflow and reduction architectures. Today, its influence can be seen in contemporary parallel programming systems like map-reduce (FP had analogs of map and reduce, as did LISP and other functional languages).
Nevertheless, I believe Backus was mistaken in his claim that imperative languages are unsuitable for parallel programming because they “keep us thinking in word-at-a-time terms.”
To make this point, I will discuss parallel programming models for graph analytics, which is currently a hot research topic. A canonical problem in this domain is the single-source shortest-path (sssp) problem: given an undirected graph with positive edge lengths, and a source node, compute the length of the shortest path from the source to each node. There are many algorithms for sssp, ranging from the classical Dijkstra and Bellman-Ford algorithms, which are taught in undergraduate algorithms courses, to more recent ones like delta-stepping.
The standard way of describing these algorithms is to use pseudocode, but this obscures the deep connections between them and makes parallelism opaque, as Backus told us.
Here is a better way: use data-centric concepts to describe algorithms. There are three key concepts – active nodes, operator, and schedule – which are the data-centric analogs of the program counter, assignment statement, and flow-of-control respectively.
Active nodes are sites in the graph where there is work to be performed. In sssp algorithms, each node u is given a label d(u) that keeps track of the length of the shortest known path to that node. This label is initialized to a large positive number at all nodes other than the source, whose label is set to zero. During execution, a node label may be updated, in which case the node is said to become active, and it is put on a worklist. Initially, only the source node is active; algorithms terminates when there are no active nodes left.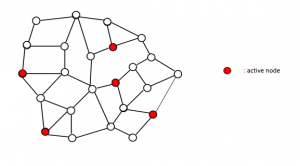
Figure 1: Active nodes
The operator is a state update that is applied to an active node. Algorithms for sssp use the relaxation operator: to process an active node u, each of its neighbors v is examined, and d(v) is lowered to d(u)+length(u,v) if this value is smaller than d(v), making v active. An active node becomes inactive when the operator has been applied to it, although it may be reactivated later in the execution.
Since there may be many active nodes at any point during execution, we must also specify the order or schedule in which active nodes should be processed from the worklist. Different scheduling policies give rise to a different sssp algorithms, some of which are listed below.
- Select an active node at random from the worklist. This is called chaotic relaxation; it is easy to implement but its running time can be exponential in the size of the graph since a node can be relaxed many times.
- Select an active node with the smallest label. This node’s label must have reached its final value so each node is relaxed at most once if this scheduling policy is used. This is Dijkstra’s algorithm, and the worklist is implemented using a min-priority queue.
- A compromise between these extremes is to treat labels as soft priorities: try to process active nodes in increasing order of label values but allow a controlled number of priority inversions. This is the idea behind delta-stepping.
Decomposing algorithms in this way into operators and schedules brings out the similarities and differences between sssp algorithms: notice that all of them use the same operator but different scheduling policies.
Since each operator application updates a small region of the graph surrounding the active node, parallelism can be exploited by processing multiple active nodes from the worklist simultaneously. The ordering constraints specified by the algorithm must still be respected; for example, in Dijkstra’s algorithm, all nodes with the smallest label can be processed in parallel. To ensure that the semantics of the operator are respected, the operator must execute atomically. In addition, the graph and worklist data structures must support this fine-grain “amorphous data-parallelism” (for example, the graph should not be implemented with a single global lock).
Algorithms for other graph analytics problems like connected components or page-rank use different operators but parallel data structures like the graph and worklists can be reused across algorithms. In fact, this operator formulation of algorithms is useful in many other domains including stencil codes, finite-elements, n-body methods, circuit design tools, and machine learning. In some of these applications such as finite-element mesh generation and refinement, operators may update the graph structure by adding and removing nodes and edges. In applications like stencil codes, the data structure is a grid rather than an unstructured graph, and parallelism can be found using static analysis of programs. Nevertheless, the idea of formulating algorithms in data-centric terms by decomposing them into operators and schedules still applies and provides a systematic approach to exploiting parallelism and locality.
Unlike Backus’s FP, this data-centric programming model is imperative, and it can be implemented using programming patterns in conventional languages like C++. Programs written in this model have been shown to scale to hundreds of cores on NUMA shared-memory machines and some programs to nearly a hundred thousand cores on large-scale distributed-memory clusters.
So was Backus wrong when he told us that imperative languages keep us thinking in “word-at-time programming”? I think he was right if by imperative languages, we mean imperative programming models based on the traditional concepts of the program counter, assignment statement and flow-of-control constructs. However, if we replace these concepts with the data-centric concepts of active nodes, operators and schedules respectively, imperative languages do not tie us down to word-at-a-time programming.
I don’t know if Backus would have agreed with me, but I think that as the inventor of FORTRAN, the first high-level imperative programming language, he may have been secretly pleased!
About the Author: Keshav Pingali (pingali@cs.utexas.edu) is a professor in the CS department and ICES at the University of Texas at Austin.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


