Continuing with our thread on looking past abstractions in quantum computing, guest bloggers Yunong Shi from EPiQC and Christopher Chamberland and Andrew Cross from IBM examine how to make qubits fault tolerant by exploiting more of the physical state space available in quantum circuits.
Qubits are the most basic elements of quantum computing, just like classical bits for classical computers. However, there are two major differences between the two. First, it is well known that qubits, inherently, can be in a superposition of logical 0 or 1 states as opposed to be in just one of them. Second, from an engineering point of view, we might never be able to manufacture (physical) qubits as reliably as classical bits we have today. To illustrate the difference, we can compare the quality of the first-generation of both. The first classical bits used on the giant ENIAC machine are a room of vacuum tubes (around 17000 in total). On average, there was only one tube that fails every two days. On the other hand, for the first generation of qubits we have now, the average lifetime is on the scale of a millisecond to second, depending on the technology, but in any case, it means after about one hundred to one thousand operations, all qubits are expected to fail. Also, the fidelity drop of qubits is a continuous process (so the “lifetime” is actually defined to be the point in time where the fidelity decay drops to 1/e), so your computation is corrupted the moment after you initialize your qubits.
Because of their robustness, in classical computing we do not care about the physical condition of the bits except the 0/1 values that they store. However, the fragility of qubits make error mitigation and error correction an irreplaceable part of the computation. Can/Should we extract more information from each of our qubits to monitor their internal correctness and assist higher level error processing? Error correction schemes use redundant qubits to encode the information and then can afford to make measurements to collapse to a subspace and extract error messages. Here what we ask is more about the physics of individual qubits. Is there any redundancy inside qubits that we should take advantage? To answer these questions, let’s first examine some current qubit implementations.
In principle, any physical system with two different energy levels can be used as a qubit. For example, the celebrated transmon qubits use the lowest two energy levels of the charge states in superconducting LC circuits with Josephson junctions; trapped ion qubits can be encoded in two ground-state hyperfine levels or a ground state level and an excited level of an ion; quantum dot qubits use two electron spin triplet states. These information processing platforms have rather distinct physical characteristics, however, they all can encode a qubit.
Notice that these traditional implementations only use a small part of the physical space for storing the quantum information. To explain what it means, we will elaborate on the superconducting qubits as an example. Before we jump into quantum LC circuits, we can first consider a classical LC circuit. We know from high school that the equation of motion for LC circuits is the same as that of a pendulum (with a small displacement) or a spring. These are all examples of harmonic oscillators. The voltage across the elements are oscillating sinusoidally and the current is oscillating cosinusoidally. If we plot the voltage (displacement, denoted as “Q”) and current (speed, denoted as “P”) of a LC circuit (a pendulum) at different time versus each other, the points will form a circle (up to normalization) as illustrated below, and this plot is often referred as the phase space diagram. If the amplitude of the oscillation is higher (which implies the system energy is higher), the radius of the circle is larger. The motion with the lowest energy is a single point at the origin.
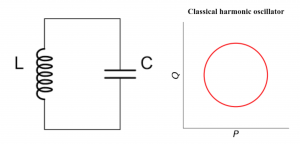
Superconducting qubits are based on the quantized version of the LC circuits, where one of the quantized values is the energy. Thus, the “height” of the quantum oscillator can only take discrete values. What’s more, the phase space diagram is not a circle anymore but a (quasi-)probability distribution in the phase space. We added the prefix “quasi-” here because the probability can be negative. We can look at the phase space diagram for the quantum motion with the lowest energy (which is called the ground state) and the motion with the second lowest energy (called first excited state), which are obtained by solving the Schrodinger’s equation. In the following plots, red means positive probability, blue means negative probability and intensity indicates the numerical value.
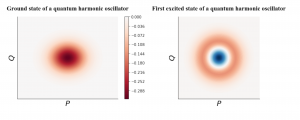
With the ability to prepare and manipulate these two states, we can encode a qubit in the quantum LC circuit with the ground state as our logic 0 and the first excited state as our logic 1. For example, we can have some electronic signals that happen to provide the energy difference
![]()
between the two states (see figure below) then we can excite the qubit from the ground state to the first excited state, thus achieve the NOT gate:
![]()
But there is one more thing that we overlooked, that is the quantum harmonic oscillator has many levels and all the energy levels are equally spaced. Then:
![]()
will also transform
![]()
Similarly, it will make the transformation
![]()
In both cases, it brings the state out of the logical space. We refer to this kind of error as leakage errors.
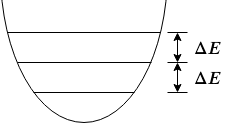
So we need to make some changes. One solution is to replace the inductor in the LC circuit with an element called the “Josephson junction”, which is devised by Brian Josephson in 1962 and won him the Nobel prize in 1973. The inclusion of the Josephson junction turns the quantum harmonic oscillator into a quantum anharmonic oscillator in which the energy levels are not equal spacing anymore (thus “anharmonic”). This is analogous to a pendulum. In this way, we can selectively address the energy levels of interest. This design is the predecessor of the transmon qubit called the Cooper pair box. However, even in this case, we cannot completely mitigate leakage errors.
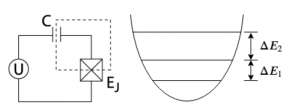
At this point, we explained why the leading types of qubits only use part of the physical space and why leakage error could potentially be a problem. Now we come back to our original question: is there any way that a qubit can be defined to use the whole physical space in a way that leakage errors are avoided and the redundant space may even provide us other error information?
Well, there are many ways that we can use the whole physical space, but there is a fundamental difficulty preventing us from extracting the error information — the Heisenberg uncertainty principle. The Heisenberg uncertainty principle states that we cannot both be certain about the distribution along the P and Q direction. For example, we can “squeeze” the distribution of the P direction of the ground state of a harmonic oscillator. Then if we measure the P axis, the outcome will have a high probability of being near 0, but the measurement outcomes in Q axis spread. Usually we need both P and Q information to completely describe the error messages unless we know that the error is biased.
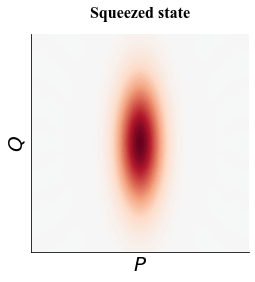
To overcome the restriction brought by the Heisenberg uncertainty principle, Daniel Gottesman, Alexei Kitaev and John Preskill came up a beautiful idea that has recently been called the grid state or the GKP state. We can take a look at its phase space diagram.
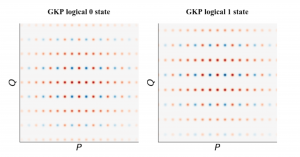
The grid coordinates of the logical 0 state are
![]()
and the grid coordinates of the logical 1 state are
![]()
With the grid states, we are still uncertain about the P and Q coordinates, but somehow we can detect the errors in both directions, because even though we do not know which peak we will be measuring, we know that it must be multiples of:
![]()
For example, we could measure an unknown GKP state to have Q coordinate of:
![]()
no matter which outcome it is, we know that there must be an error of:
![]()
then we can shift its Q value back by the same value, which is not hard to do experimentally.
It turns out the P, Q coordinate information that GKP qubits provide is also extremely useful to an upper-level error correction code. Several works [1][2][3] explored the idea of combining a surface code and GKP qubits and found that, with the additional continuous information of the P, Q value in the surface code stabilizer measurement, fault tolerance can be improved. Now, we can answer the question asked in the beginning: can we extract more information from a qubit to assist higher level error correction? The answer is yes, and it may help us build a reliable quantum computer sooner.
A downside of the GKP qubits though is that they are highly non-classical, thus making them is a non-trivial task. For example, using superconducting resonators, the high photon number in GKP states makes the usual first-order analysis fail. In recent work, we gave fault-tolerance definitions that apply to the GKP state preparation task on superconducting platforms, and we performed higher-order analysis to understand how errors impact the GKP state.
With error mitigation and error correction being a crucial part of the computation, we expect alternative qubit architectures like the ones described in this blog to be strong candidates to explore for useful and reliable quantum computing.
About the Authors:
Yunong Shi is a senior graduate student on the EPiQC Project advised by Fred Chong. He is on the job market this year. His work spans quantum control pulse optimization, fault-tolerant qubits, quantum chemistry encodings, and formal verification of quantum compilers.
Christopher Chamberland is a research staff member in the quantum computing group at IBM working on quantum error correction and fault-tolerant quantum computing.
Andrew Cross is a research staff member and manager of the theory of quantum computing and information group at IBM’s T.J. Watson Research Center.
Fred Chong is the Seymour Goodman Professor of Computer Architecture at the University of Chicago. He is the Lead Principal Investigator of the EPiQC Project (Enabling Practical-scale Quantum Computation), an NSF Expedition in Computing and a member of the STAQ Project.
(Cover image credit: Yongshan Ding photo from the Schuster Lab)
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


