With two blog posts, we argue for more use of simple models beyond Amdahl’s Law. Part 1 previously discussed Bottleneck Analysis and Little’s Law, while this post (Part 2) presents the M/M/1 Queue.
Previously, Part 1 of these two blog posts provided our thesis that analytic models can complement measurement and simulations to give quick insight, show what is not possible, provide a double-check, and suggest future directions. It also presented Bottleneck Analysis and Little’s Law that can give initial answers to questions like:
- What is the maximum throughput through several subsystems in series and parallel?
- How many buffers are needed to track pending requests as a function of needed bandwidth and expected latency?
In this Part 2, we conclude by presenting the M/M/1 Queue, which shows the answer to this third question is “no”:
3. Can one both minimize latency and maximize throughput for unscheduled work?
While Little’s Law provides a black-box result, it does not expose tradeoffs. The M/M/1 queue will show us a required trade-off among (a) allowing unscheduled task arrivals, (b) minimizing latency, and (c) maximizing throughput.
To be more precise, let’s posit that “unscheduled task arrivals” means this property: When a task arrives is independent (unaffected) of when previous tasks arrived. For example, my user request doesn’t know when you made yours. Queuing Theory has named this property “Markovian” (or equivalently “Poisson arrivals” or “exponential inter-arrival times”).
Figure 1 depicts a simple queue where tasks arrive, are optionally queued in the buffers to the left if the server is already busy, are then serviced one at a time in the circular server, and depart to the right. Let tasks arrive at rate R, optionally wait for average queuing time Q, and be serviced (without further queuing) at average time S. Let L denoted the average total latency to handle a task, equal to Q + S. We simplify from standard queueing theory notation that usually denotes R as λ and 1/S as μ.
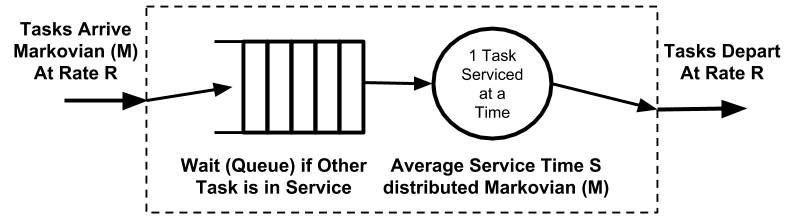
Figure 1: M/M/1 Queue
Figure 1’s queue becomes M/M/1 with three further assumptions: tasks arrive Markovian (1st M), are serviced Markovian (2nd M), and are serviced one at a time (final 1). The middle assumption—that tasks are serviced Markovian—seems strange but is an effective model of service time variability (whereas assuming all service times always equal S is usually optimistic). The M/M/1 queue also assumes that the arrival rate is not affected by the unbounded number of tasks in the queue (called an “open system”).
Figure 2 plots the M/M/1 queue’s latency-throughput trade-off. The x-axis is the fraction of maximum throughput achieved x = R*S. The y-axis is average total latency (L)—queuing plus service—normalized by dividing the no-waiting service time (S) for y = L/S. Thus, y = 1 means no waiting. Finally, queuing theory queuing theory provides the plotted curve as L/S = 1/(1-R*S) or more simply y = 1/(1-x). (FYI: x is the fraction of maximum throughput achieved, because (a) the actual throughput matches the arrival rate R, (b) maximum throughput is 1/S as the reciprocal of one-at-a-time average service time S, and (c) so the fraction of throughput is R/(1/S) = R*S.)
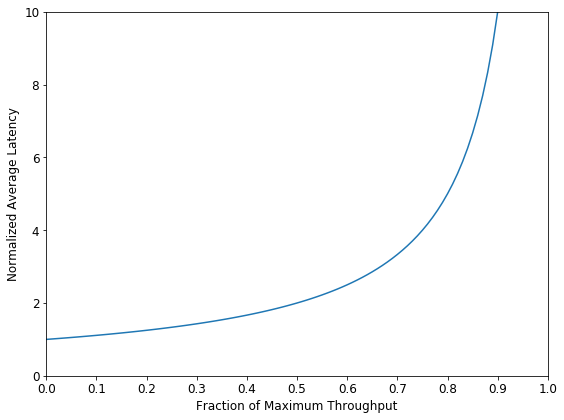
Figure 2: M/M/1 Queue Latency vs. Throughput Tradeoff
Importantly, Figure 2 reveals:
High throughput ⇒ high latency: As the fraction of maximum throughput approaches 1, latency explodes toward infinity, making full throughput infeasible. Intuitively, near-full throughput makes it harder to “recover” from a backlog of tasks after inevitable Markovian arrival bursts.
Low latency ⇒ low throughput: As throughput approaches 0, normalized latency approaches 1 where there is no queuing delay before service (i.e., arrivals rarely wait for previous tasks).
Intermediate latency/throughput values reveal a stark trade-off: Throughput fractions 0.25, 0.50, 0.75, and 0.90 see normalized latencies of 1.33, 2.00, 4.00, and 10.00, respectively.
Consider an example of applying an M/M/1 queue. Assume that a computer must handle network packets arriving unscheduled at a rate R = 10 packets/second with a goal of handling each packet with a total latency (including waiting) of L = 100 ms. How long can the computer take to process (service) each packet (not counting waiting), denoted S? A first answer might set S = 100 ms, as that is the average time between packet arrivals.
For unscheduled arrivals, however, M/M/1 warns us that the above design will fail as maximal throughput causes exploding latency. Instead with M/M/1, we must service each packet in an average of S = 50 ms with 50 ms average delay for queuing and 50% of maximum throughput. (To double-check, solve for S in L/S = 1/(1-R*S) when R = 10 packets/second and L = 100 ms.) The M/M/1 design seems to over-designed by 2x (100ms → 50ms), but this is actually necessary.
For the previous cache miss buffer example, the 32-buffer answer is minimal for 100-ns average miss latency. Nevertheless, it would be prudent to increase buffering (e.g. another 50% to 48) to handle inevitable arrival bursts, unpredictable miss latency, or both.
On the other hand, to achieve low latency and highest bandwidth together, one must discard an M/M/1 queue and coerce task arrivals to not be Markovian and, in the best case, be scheduled (e.g., like at the dentist). Good online introductions to queuing theory include Lazowska, et al. and Tay.
Please keep the M/M/1 Queue, as well as Bottleneck Analysis and Little’s Law from Part 1, in mind during the next presentation with numbers that seem too good to believe. We thank Dan Gibson, Swapnil Haria, Matt Sinclair, Guri Sohi, Daniel Sorin, and Juliette Walker for improving both blog posts and a four-page arXiv paper that includes all three models.
About the Author: Mark D. Hill is John P. Morgridge Professor and Gene M. Amdahl Professor of Computer Sciences at the University of Wisconsin-Madison. He is a fellow of IEEE and the ACM, serves as Chair of the Computer Community Consortium (2018-20) and served as Wisconsin Computer Sciences Department Chair 2014-17.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


